# DiffEqFlux.jl

[![Join the chat at https://gitter.im/JuliaDiffEq/Lobby](https://badges.gitter.im/JuliaDiffEq/Lobby.svg)](https://gitter.im/JuliaDiffEq/Lobby?utm_source=badge&utm_medium=badge&utm_campaign=pr-badge&utm_content=badge)
[![Build Status](https://travis-ci.org/JuliaDiffEq/DiffEqFlux.jl.svg?branch=master)](https://travis-ci.org/JuliaDiffEq/DiffEqFlux.jl)
[![Build status](https://ci.appveyor.com/api/projects/status/e5a9pad58ojo26ir?svg=true)](https://ci.appveyor.com/project/ChrisRackauckas/diffeqflux-jl)

DiffEqFlux.jl fuses the world of differential equations with machine learning
by helping users put diffeq solvers into neural networks. This package utilizes
[DifferentialEquations.jl](http://docs.juliadiffeq.org/latest/) and
[Flux.jl](https://fluxml.ai/) as its building blocks.

## Example Usage

For an overview of what this package is for, [see this blog post]().

### Optimizing parameters of an ODE

First let's create a Lotka-Volterra ODE using DifferentialEquations.jl. For
more details, [see the DifferentialEquations.jl documentation]()

```julia
using DifferentialEquations
function lotka_volterra(du,u,p,t)
  x, y = u
  α, β, δ, γ = p
  du[1] = dx = α*x - β*x*y
  du[2] = dy = -δ*y + γ*x*y
end
u0 = [1.0,1.0]
tspan = (0.0,10.0)
p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(lotka_volterra,u0,tspan,p)
sol = solve(prob,Tsit5())
using Plots
plot(sol)
```

![LV Solution Plot](https://user-images.githubusercontent.com/1814174/51388169-9a07f300-1af6-11e9-8c6c-83c41e81d11c.png)

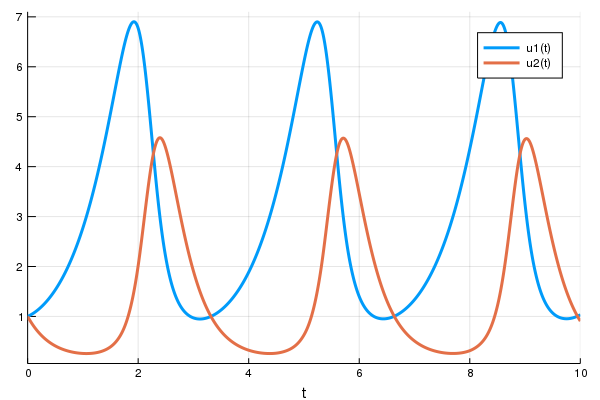
Next we define a single layer neural network that uses the `diffeq_rd` layer
function that takes the parameters and returns the solution of the `x(t)`
variable. Instead of being a function of the parameters, we will wrap our
parameters in `param` to be tracked by Flux:

```julia
using Flux, DiffEqFlux
p = param([2.2, 1.0, 2.0, 0.4]) # Initial Parameter Vector
params = Flux.Params([p])

function predict_rd() # Our 1-layer neural network
  Array(diffeq_rd(p,prob,Tsit5(),saveat=0.1))
end
```

Next we choose a loss function. Our goal will be to find parameter that make
the Lotka-Volterra solution constant `x(t)=1`, so we defined our loss as the
squared distance from 1:

```julia
loss_rd() = sum(abs2,x-1 for x in predict_rd())
```

Lastly, we train the neural network using Flux to arrive at parameters which
optimize for our goal:

```julia
data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function () #callback function to observe training
  display(loss_rd())
  # using `remake` to re-create our `prob` with current parameters `p`
  display(plot(solve(remake(prob,p=Flux.data(p)),Tsit5(),saveat=0.1),ylim=(0,6)))
end

# Display the ODE with the initial parameter values.
cb()

Flux.train!(loss_rd, params, data, opt, cb = cb)
```

![Flux ODE Training Animation](https://user-images.githubusercontent.com/1814174/51399500-1f4dd080-1b14-11e9-8c9d-144f93b6eac2.gif)

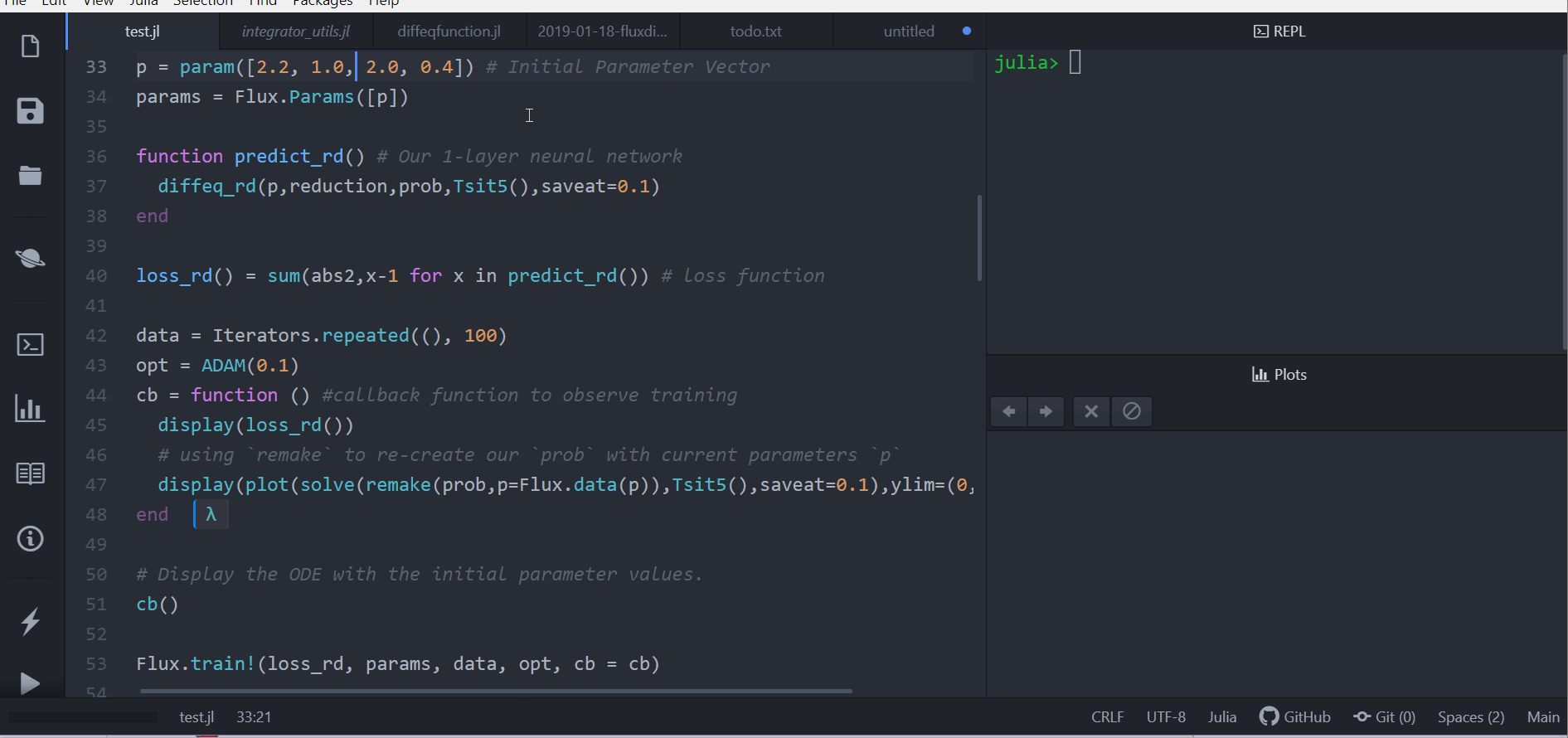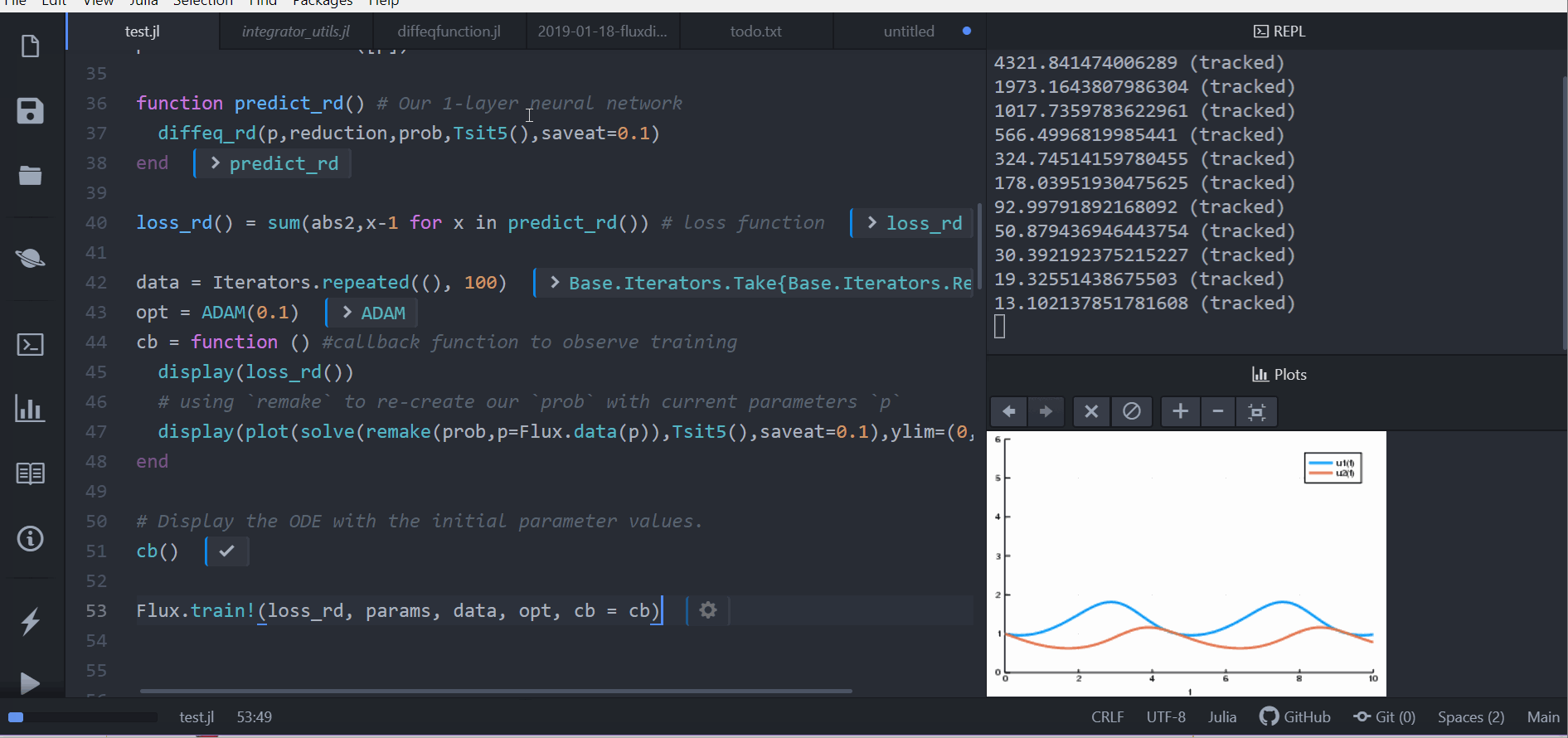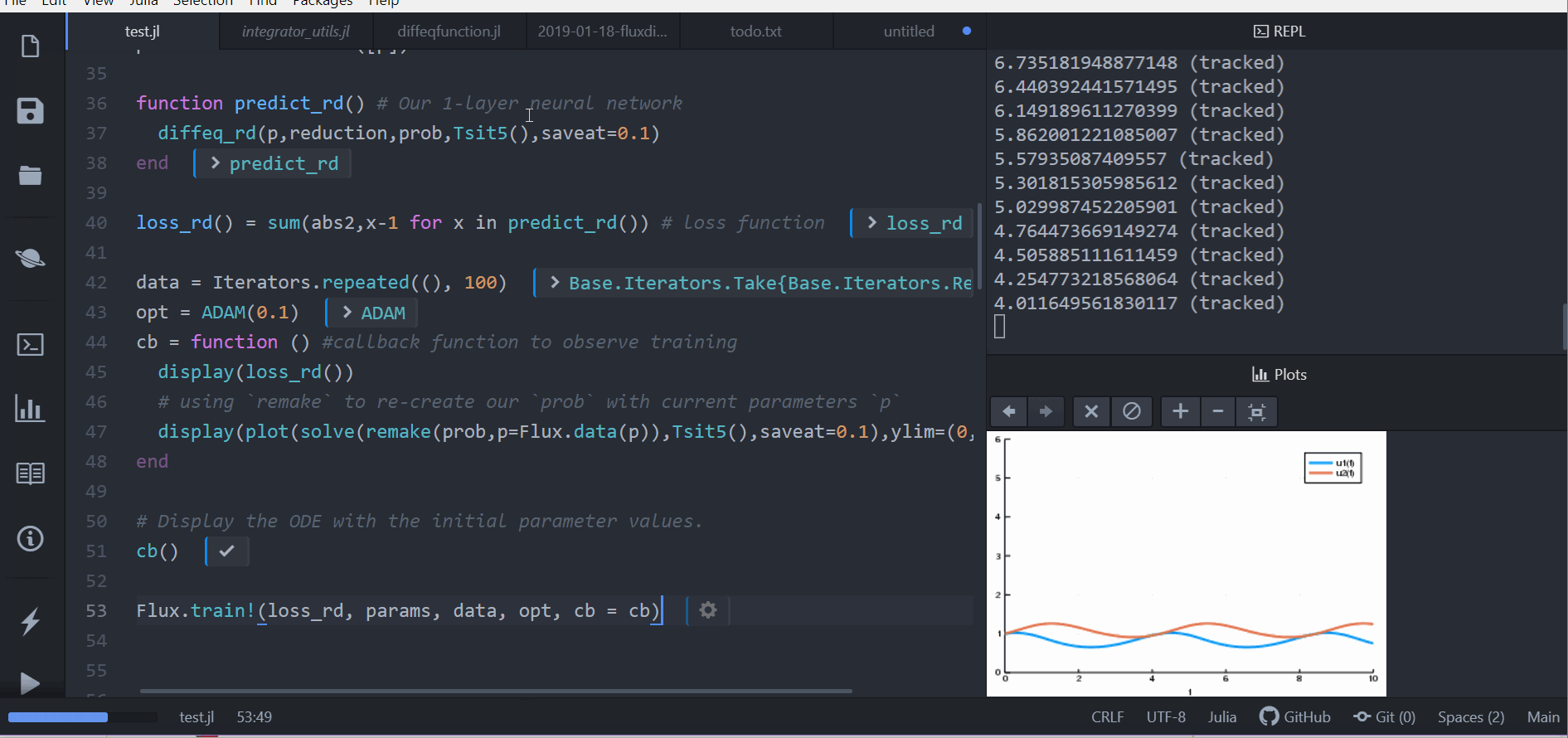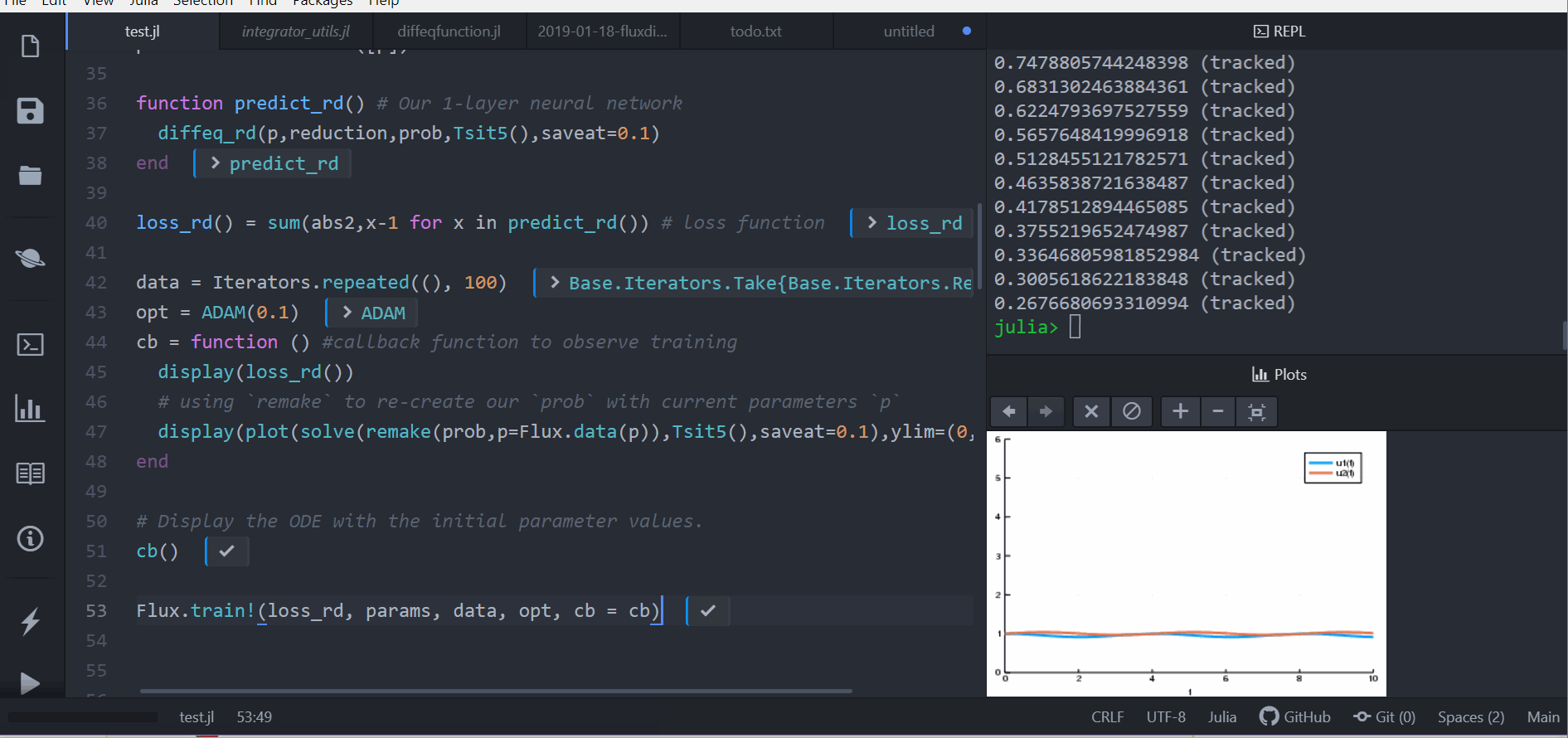
Note that by using anonymous functions, this `diffeq_rd` can be used as a
layer in a neural network `Chain`, for example like

```julia
m = Chain(
  Conv((2,2), 1=>16, relu),
  x -> maxpool(x, (2,2)),
  Conv((2,2), 16=>8, relu),
  x -> maxpool(x, (2,2)),
  x -> reshape(x, :, size(x, 4)),
  # takes in the ODE parameters from the previous layer
  p -> Array(diffeq_rd(p,prob,Tsit5(),saveat=0.1),
  Dense(288, 10), softmax) |> gpu
```

or

```julia
m = Chain(
  Dense(28^2, 32, relu),
  # takes in the initial condition from the previous layer
  x -> Array(diffeq_rd(p,prob,Tsit5(),saveat=0.1,u0=x))),
  Dense(32, 10),
  softmax)
```

### Using Other Differential Equations

Other differential equation problem types from DifferentialEquations.jl are
supported. For example, we can build a layer with a delay differential equation
like:

```julia
function delay_lotka_volterra(du,u,h,p,t)
  x, y = u
  α, β, δ, γ = p
  du[1] = dx = (α - β*y)*h(p,t-0.1)[1]
  du[2] = dy = (δ*x - γ)*y
end
h(p,t) = ones(eltype(p),2)
prob = DDEProblem(delay_lotka_volterra,[1.0,1.0],h,(0.0,10.0),constant_lags=[0.1])

p = param([2.2, 1.0, 2.0, 0.4])
params = Flux.Params([p])
function predict_rd_dde()
  Array(diffeq_rd(p,prob,MethodOfSteps(Tsit5()),saveat=0.1))
end
loss_rd_dde() = sum(abs2,x-1 for x in predict_rd_dde())
loss_rd_dde()
```

Or we can use a stochastic differential equation:

```julia
function lotka_volterra_noise(du,u,p,t)
  du[1] = 0.1u[1]
  du[2] = 0.1u[2]
end
prob = SDEProblem(lotka_volterra,lotka_volterra_noise,[1.0,1.0],(0.0,10.0))

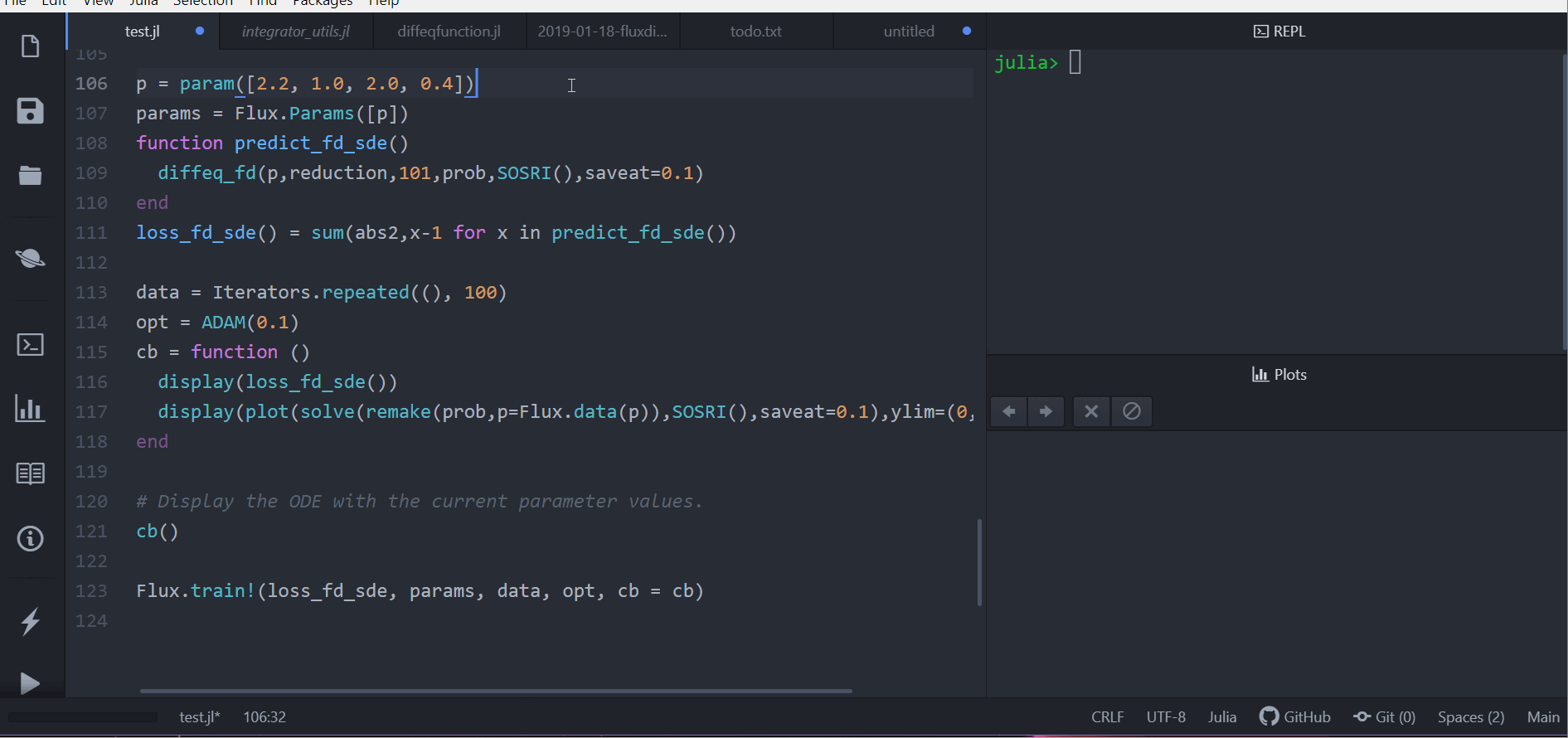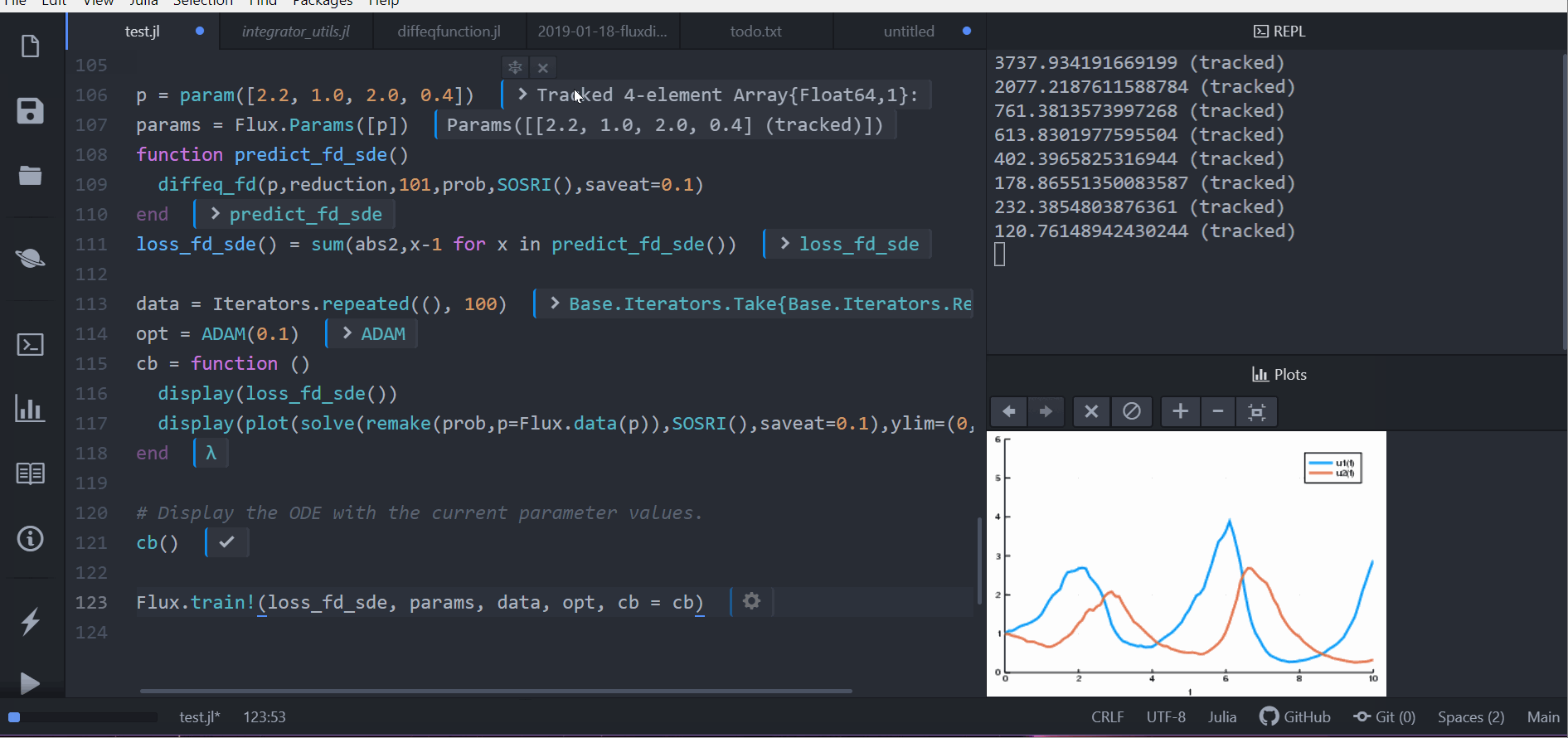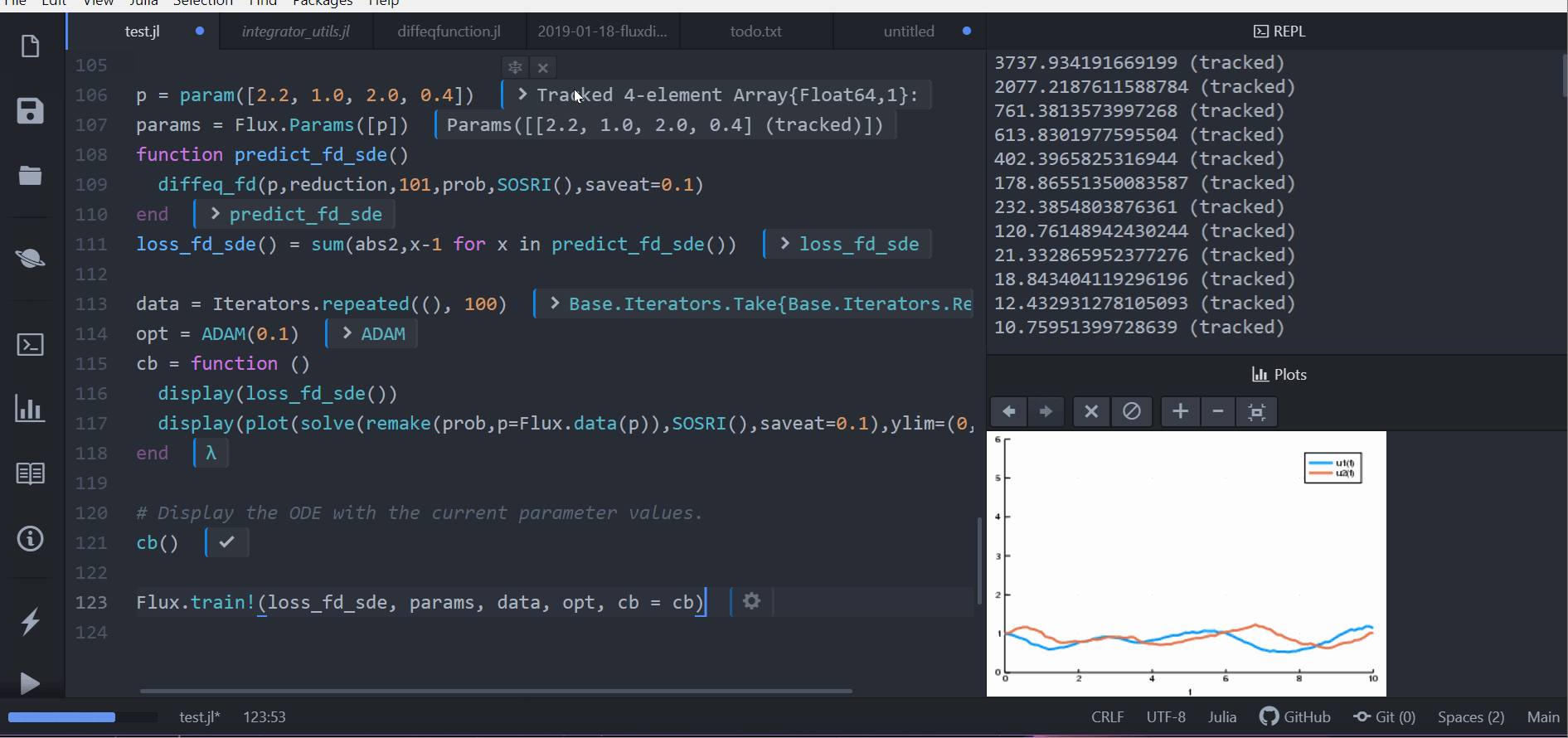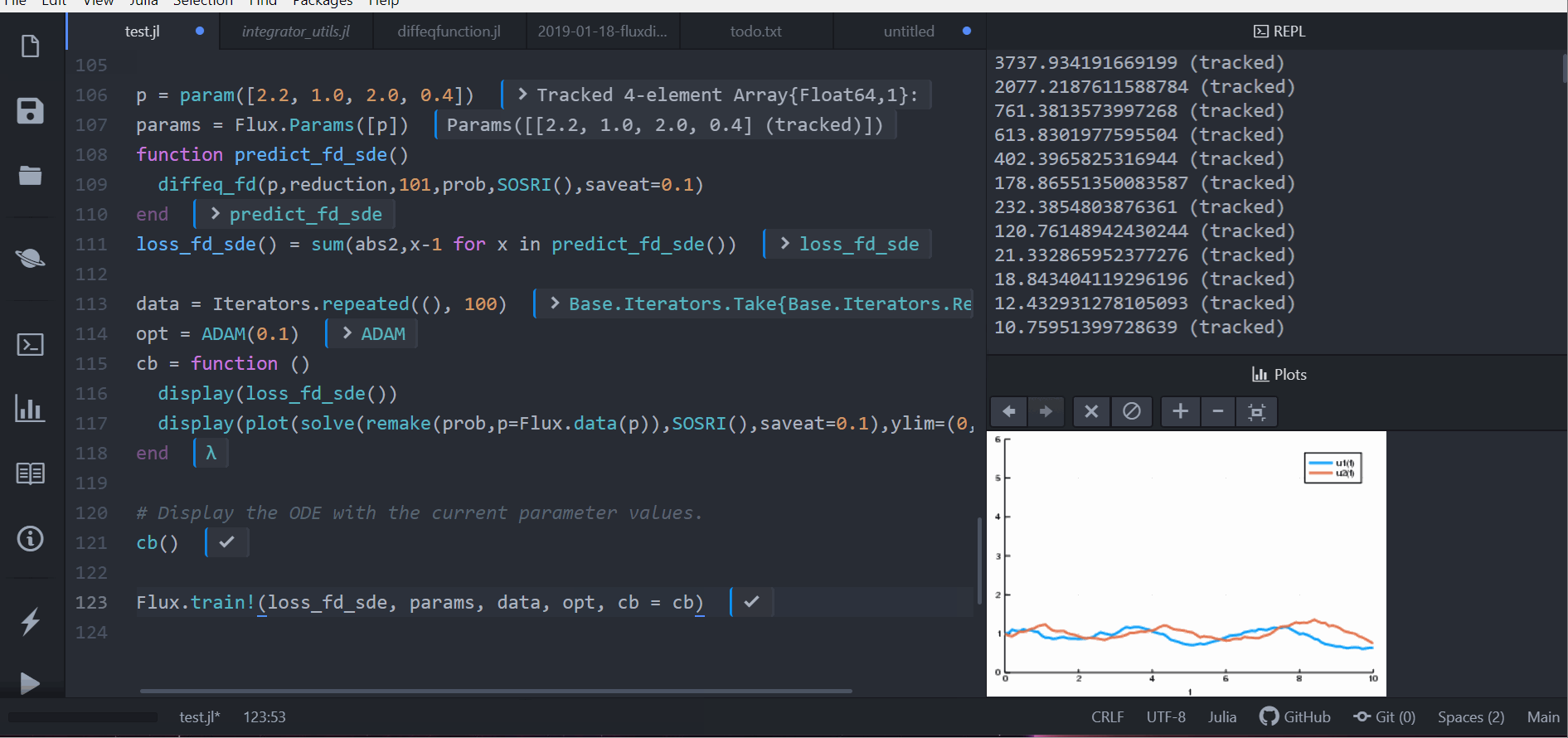
p = param([2.2, 1.0, 2.0, 0.4])
params = Flux.Params([p])
function predict_fd_sde()
  diffeq_fd(p,reduction,101,prob,SOSRI(),saveat=0.1)
end
loss_fd_sde() = sum(abs2,x-1 for x in predict_fd_sde())
loss_fd_sde()

data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function ()
  display(loss_fd_sde())
  display(plot(solve(remake(prob,p=Flux.data(p)),SOSRI(),saveat=0.1),ylim=(0,6)))
end

# Display the ODE with the current parameter values.
cb()

Flux.train!(loss_fd_sde, params, data, opt, cb = cb)
```

![SDE NN Animation](https://user-images.githubusercontent.com/1814174/51399524-2c6abf80-1b14-11e9-96ae-0192f7debd03.gif)

### Neural Ordinary Differential Equations

We can use DiffEqFlux.jl to define, solve, and train neural ordinary differential
equations. A neural ODE is an ODE where a neural network defines its derivative
function. Thus for example, with the multilayer perceptron neural network
`Chain(Dense(2,50,tanh),Dense(50,2))`, a neural ODE would be defined as having
the ODE function:

```julia
model = Chain(Dense(2,50,tanh),Dense(50,2))
# Define the ODE as the forward pass of the neural network with weights `p`
dudt_(du,u,p,t) = du .= model(u)
```

A convenience function which handles all of the details is `neural_ode`. To
use `neural_ode`, you give it the initial condition, the internal neural
network model to use, the timespan to solve on, and any ODE solver arguments.
For example, this neural ODE would be defined as:

```julia
tspan = (0.0f0,25.0f0)
x->neural_ode(x,dudt,tspan,Tsit5(),saveat=0.1)
```

where here we made it a layer that takes in the initial condition and spits
out an array for the time series saved at every 0.1 time steps.

### Training a Neural Ordinary Differential Equation

Let's get a time series array from the Lotka-Volterra equation as data:

```julia
function lotka_volterra(du,u,p,t)
  x, y = u
  α, β, δ, γ = p
  du[1] = dx = α*x - β*x*y
  du[2] = dy = -δ*y + γ*x*y
end
u0 = [1.0,1.0]
tspan = (0.0,10.0)
p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(lotka_volterra,u0,tspan,p)
ode_data = Array(solve(prob,Tsit5(),saveat=0.1))
```

Now let's define a neural network with a `neural_ode` layer. First we define
the layer:

```julia
dudt = Chain(Dense(2,50,tanh),Dense(50,2))
tspan = (0.0f0,10.0f0)
n_ode = x->neural_ode(x,dudt,tspan,Tsit5(),saveat=0.1)
```

And build a neural network around it. We will use the L2 loss of the network's
output against the time series data:

```julia
function predict_n_ode()
  n_ode(u0)
end
loss_n_ode() = sum(abs2,ode_data .- predict_n_ode())
```

and then train the neural network to learn the ODE:

```julia
data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function () #callback function to observe training
  display(loss_n_ode())
  # plot current prediction against data
  cur_pred = predict_n_ode()
  pl = scatter(0.0:0.1:10.0,ode_data[1,:],label="data")
  scatter!(pl,0.0:0.1:10.0,cur_pred[1,:],label="prediction")
  plot(pl)
end

# Display the ODE with the initial parameter values.
cb()

Flux.train!(loss_n_ode, params, data, opt, cb = cb)
```
## Use with GPUs

Note that the differential equation solvers will run on the GPU if the initial
condition is a GPU array. Thus for example, we can define a neural ODE by hand
that runs on the GPU:

```julia
u0 = [2.; 0.] |> gpu
dudt = Chain(Dense(2,50,tanh),Dense(50,2)) |> gpu

function ODEfunc(du,u,p,t)
    du .= Flux.data(dudt(u))
end
prob = ODEProblem(ODEfunc, u0,tspan)

# Runs on a GPU
sol = solve(prob,BS3(),saveat=0.1)
```

and the `diffeq` layer functions can be used similarly. Or we can directly use
the neural ODE layer function, like:

```julia
x->neural_ode(gpu(x),gpu(dudt),tspan,BS3(),saveat=0.1)
```

## API Documentation

### DiffEq Layer Functions

- `diffeq_rd(p,prob, args...;u0 = prob.u0, kwargs...)` uses Flux.jl's
  reverse-mode AD through the differential equation solver with parameters `p`
  and initial condition `u0`. The rest of the arguments are passed to the
  differential equation solver. The return is the DESolution.
- `diffeq_fd(p,reduction,n,prob,args...;u0 = prob.u0, kwargs...)` uses
  ForwardDiff.jl's forward-mode AD through the differential equation solver
  with parameters `p` and initial condition `u0`. `n` is the output size
  where the return value is `reduction(sol)`. The rest of the arguments are
  passed to the differential equation solver.
- `diffeq_adjoint(p,prob,args...;u0 = prob.u0, kwargs...)` uses adjoint
  sensitivity analysis to  "backprop the ODE solver" via DiffEqSensitivity.jl.
  The return is the time series of the solution as an array solved with parameters
  `p` and initial condition `u0`. The rest of the arguments are passed to the
  differential equation solver or handled by the adjoint sensitivity algorithm
  (for more details on sensitivity arguments, see
  [the diffeq documentation](http://docs.juliadiffeq.org/latest/analysis/sensitivity.html#Adjoint-Sensitivity-Analysis-1))

### Neural DE Layer Functions

- `neural_ode(x,model,tspan,args...;kwargs...)` defines a neural ODE layer where
  `x` is the initial condition, `model` is a Flux.jl model, `tspan` is the
  time span to integrate, and the rest of the arguments are passed to the ODE
  solver. The parameters should be implicit in the `model`.
- `nueral_msde(x,model,mp,tspan,args...;kwargs)` defines a neural multiplicative
  SDE layer where `x` is the initial condition, `model` is a Flux.jl model,
  `tspan` is the time span to integrate, and the rest of the arguments are
  passed to the SDE solver. The noise is assumed to be diagonal multiplicative,
  i.e. the Wiener term is `mp.*u.*dW` for some array of noise constants `mp`.