# DiffEqFlux.jl

[![Join the chat at https://gitter.im/JuliaDiffEq/Lobby](https://badges.gitter.im/JuliaDiffEq/Lobby.svg)](https://gitter.im/JuliaDiffEq/Lobby?utm_source=badge&utm_medium=badge&utm_campaign=pr-badge&utm_content=badge)
[![Build Status](https://travis-ci.org/JuliaDiffEq/DiffEqFlux.jl.svg?branch=master)](https://travis-ci.org/JuliaDiffEq/DiffEqFlux.jl)
[![Build status](https://ci.appveyor.com/api/projects/status/e5a9pad58ojo26ir?svg=true)](https://ci.appveyor.com/project/ChrisRackauckas/diffeqflux-jl)

DiffEqFlux.jl fuses the world of differential equations with machine learning
by helping users put diffeq solvers into neural networks. This package utilizes
[DifferentialEquations.jl](http://docs.juliadiffeq.org/latest/) and
[Flux.jl](https://fluxml.ai/) as its building blocks.

## Problem Domain

DiffEqFlux.jl is not just for neural ordinary differential equations. DiffEqFlux.jl is for neural differential equations.
As such, it is the first package to support and demonstrate:

- Stiff neural ordinary differential equations (neural ODEs)
- Neural stochastic differential equations (neural SDEs)
- Neural delay differential equations (neural DDEs)
- Neural partial differential equations (neural PDEs)
- Neural jump stochastic differential equations (neural jump diffusions)

with high order, adaptive, implicit, GPU-accelerated, Newton-Krylov, etc. methods. For examples, please refer to
[the release blog post](https://julialang.org/blog/2019/01/fluxdiffeq). Additional demonstrations, like neural
PDEs and neural jump SDEs, can be found [at this blog post](http://www.stochasticlifestyle.com/neural-jump-sdes-jump-diffusions-and-neural-pdes/) (among many others!).

Do not limit yourself to the current neuralization. With this package, you can explore various ways to integrate
the two methodologies:

- Neural networks can be defined where the “activations” are nonlinear functions described by differential equations.
- Neural networks can be defined where some layers are ODE solves
- ODEs can be defined where some terms are neural networks
- Cost functions on ODEs can define neural networks

## Citation

If you use DiffEqFlux.jl or are influenced by its ideas for expanding beyond neural ODEs, please cite:

```
@article{DBLP:journals/corr/abs-1902-02376,
  author    = {Christopher Rackauckas and
               Mike Innes and
               Yingbo Ma and
               Jesse Bettencourt and
               Lyndon White and
               Vaibhav Dixit},
  title     = {DiffEqFlux.jl - {A} Julia Library for Neural Differential Equations},
  journal   = {CoRR},
  volume    = {abs/1902.02376},
  year      = {2019},
  url       = {http://arxiv.org/abs/1902.02376},
  archivePrefix = {arXiv},
  eprint    = {1902.02376},
  timestamp = {Tue, 21 May 2019 18:03:36 +0200},
  biburl    = {https://dblp.org/rec/bib/journals/corr/abs-1902-02376},
  bibsource = {dblp computer science bibliography, https://dblp.org}
}
```

## Example Usage

For an overview of what this package is for, [see this blog post](https://julialang.org/blog/2019/01/fluxdiffeq).

### Optimizing parameters of an ODE

First let's create a Lotka-Volterra ODE using DifferentialEquations.jl. For
more details, [see the DifferentialEquations.jl documentation](http://docs.juliadiffeq.org/latest/)

```julia
using DifferentialEquations
function lotka_volterra(du,u,p,t)
  x, y = u
  α, β, δ, γ = p
  du[1] = dx = α*x - β*x*y
  du[2] = dy = -δ*y + γ*x*y
end
u0 = [1.0,1.0]
tspan = (0.0,10.0)
p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(lotka_volterra,u0,tspan,p)
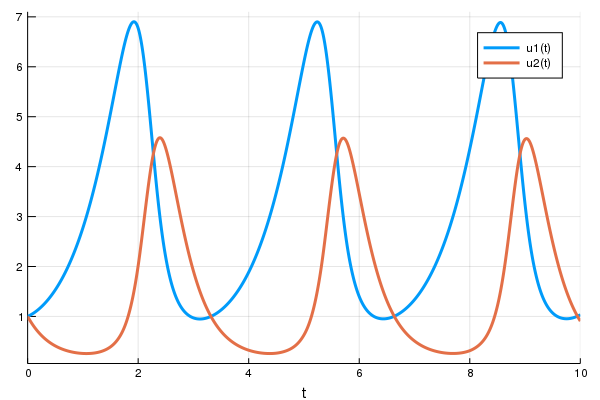
sol = solve(prob,Tsit5())
using Plots
plot(sol)
```

![LV Solution Plot](https://user-images.githubusercontent.com/1814174/51388169-9a07f300-1af6-11e9-8c6c-83c41e81d11c.png)

Next we define a single layer neural network that uses the `diffeq_rd` layer
function that takes the parameters and returns the solution of the `x(t)`
variable. Instead of being a function of the parameters, we will wrap our
parameters in `param` to be tracked by Flux:

```julia
using Flux, DiffEqFlux
p = param([2.2, 1.0, 2.0, 0.4]) # Initial Parameter Vector
params = Flux.Params([p])

function predict_rd() # Our 1-layer neural network
  Tracker.collect(diffeq_adjoint(p,prob,Tsit5(),saveat=0.0:0.1:10.0))
end
```

Next we choose a loss function. Our goal will be to find parameter that make
the Lotka-Volterra solution constant `x(t)=1`, so we defined our loss as the
squared distance from 1:

```julia
loss_adjoint() = sum(abs2,x-1 for x in predict_adjoint())
```

Lastly, we train the neural network using Flux to arrive at parameters which
optimize for our goal:

```julia
data = Iterators.repeated((), 100)
opt = ADAM(0.1)
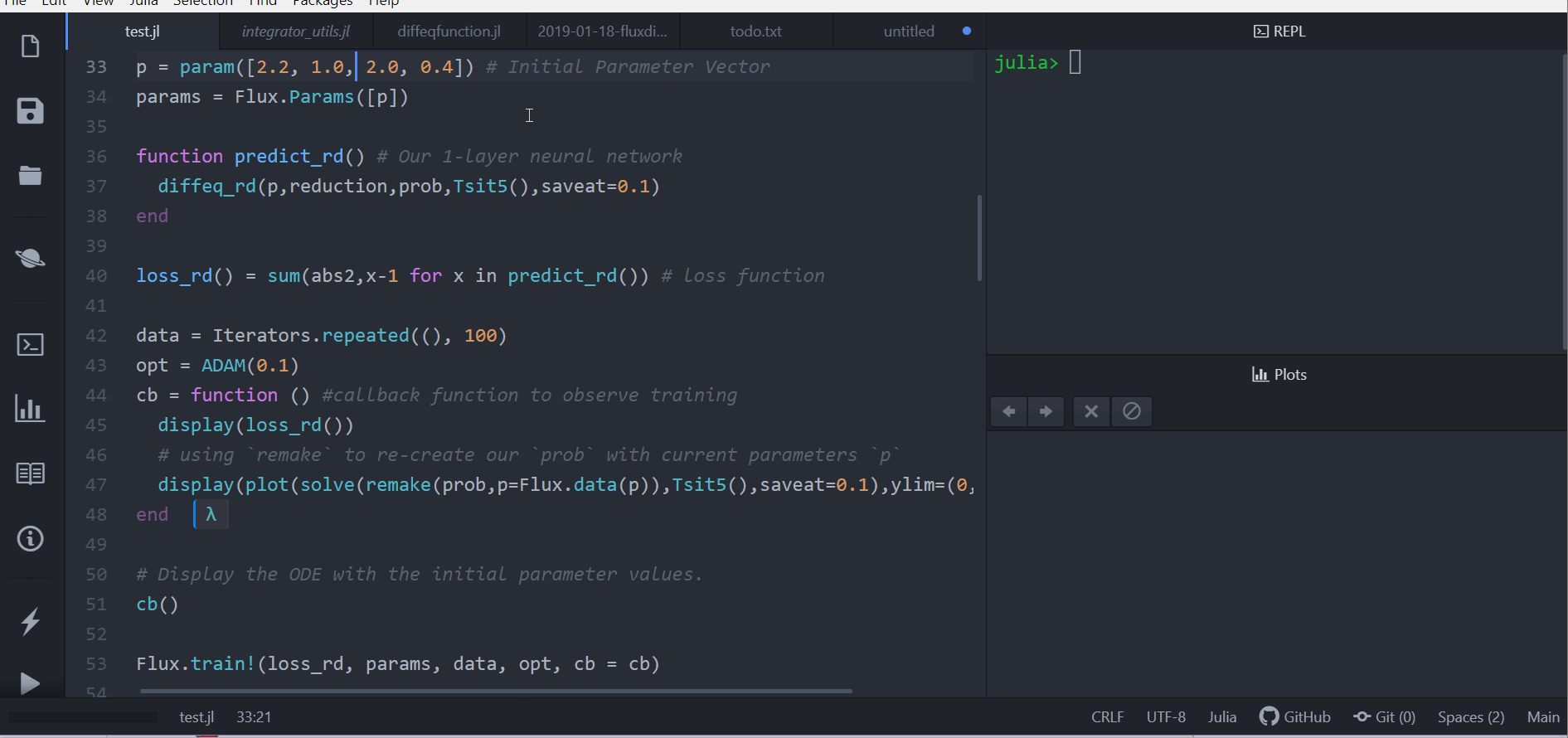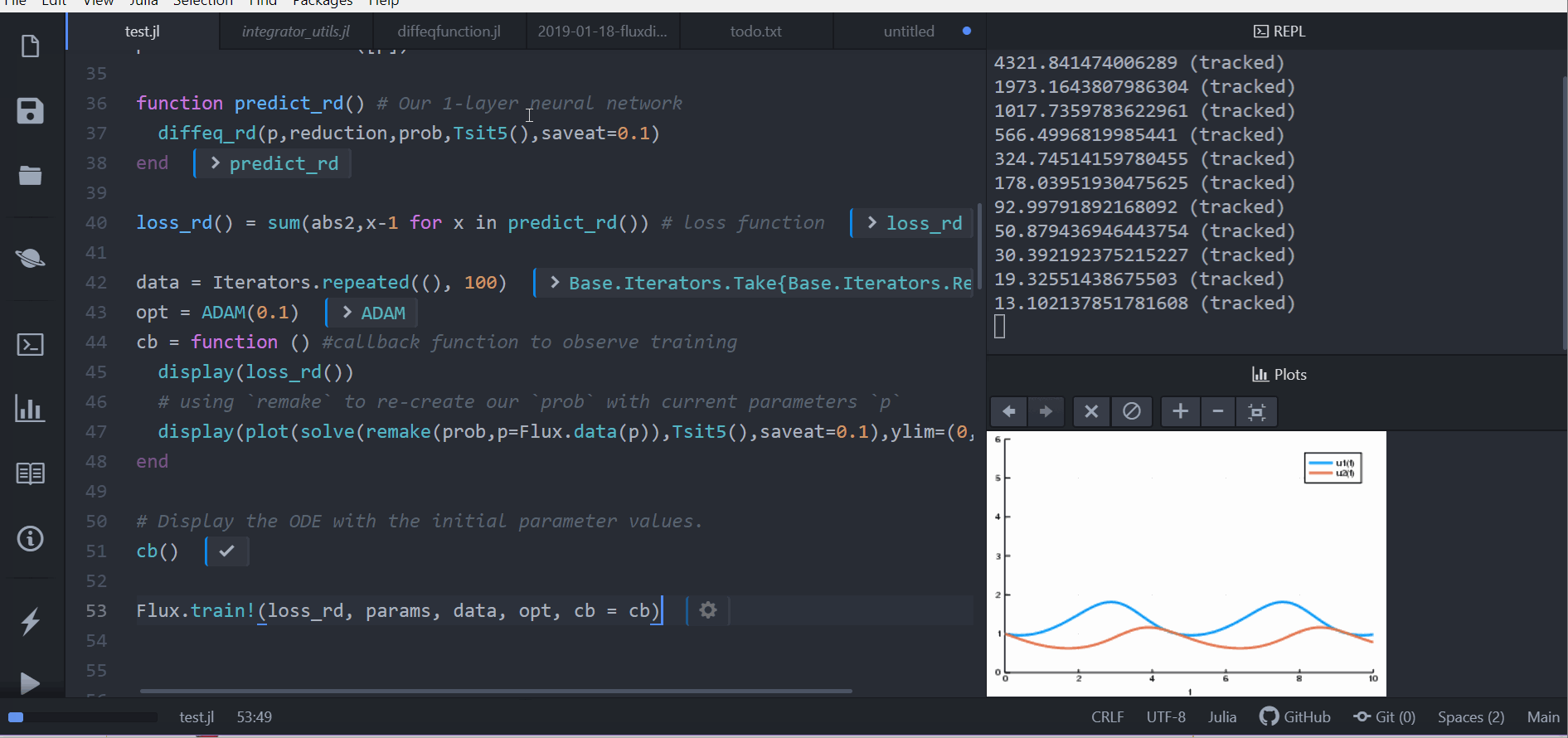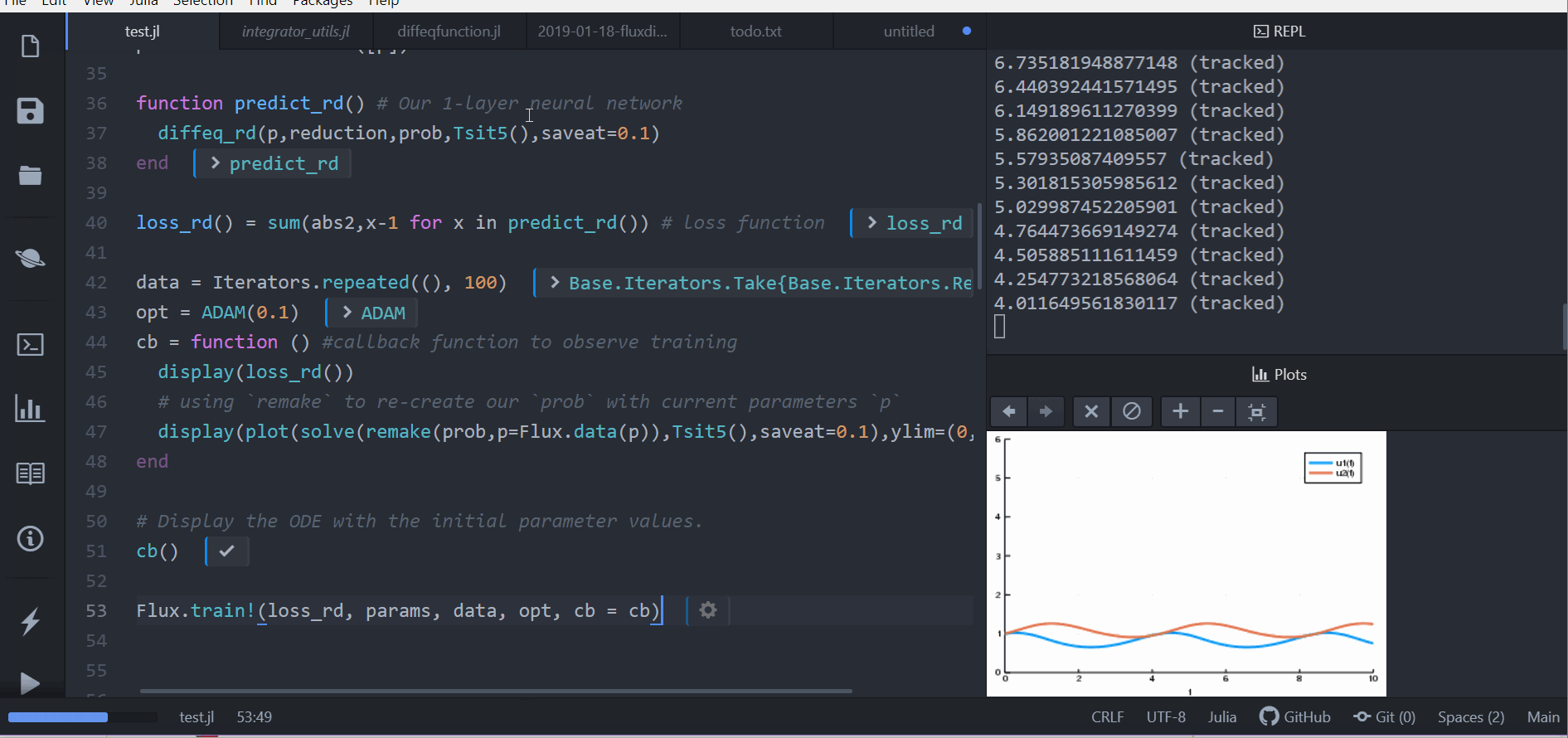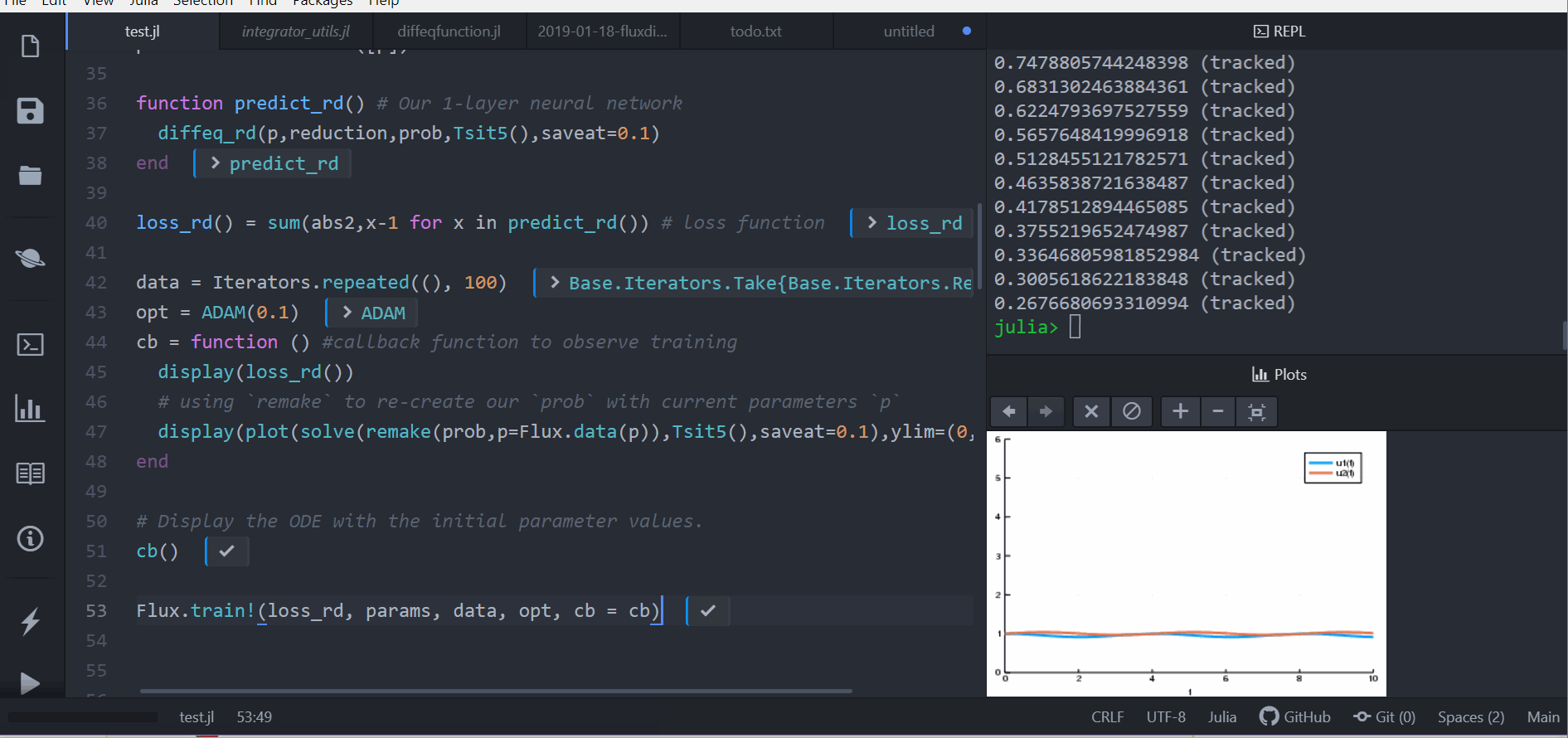
cb = function () #callback function to observe training
  display(loss_adjoint())
  # using `remake` to re-create our `prob` with current parameters `p`
  display(plot(solve(remake(prob,p=Flux.data(p)),Tsit5(),saveat=0.0:0.1:10.0),ylim=(0,6)))
end

# Display the ODE with the initial parameter values.
cb()

Flux.train!(loss_adjoint, params, data, opt, cb = cb)
```

![Flux ODE Training Animation](https://user-images.githubusercontent.com/1814174/51399500-1f4dd080-1b14-11e9-8c9d-144f93b6eac2.gif)

Note that by using anonymous functions, this `diffeq_adjoint` can be used as a
layer in a neural network `Chain`, for example like

```julia
m = Chain(
  Conv((2,2), 1=>16, relu),
  x -> maxpool(x, (2,2)),
  Conv((2,2), 16=>8, relu),
  x -> maxpool(x, (2,2)),
  x -> reshape(x, :, size(x, 4)),
  # takes in the ODE parameters from the previous layer
  p -> Array(diffeq_rd(p,prob,Tsit5(),saveat=0.1),
  Dense(288, 10), softmax) |> gpu
```

or

```julia
m = Chain(
  Dense(28^2, 32, relu),
  # takes in the initial condition from the previous layer
  x -> Array(diffeq_rd(p,prob,Tsit5(),saveat=0.1,u0=x))),
  Dense(32, 10),
  softmax)
```

Similarly, `diffeq_adjoint`, a O(1) memory adjoint implementation, can be
replaced with `diffeq_rd` for reverse-mode automatic differentiation or
`diffeq_fd` for forward-mode automatic differentiation. `diffeq_fd` will
be fastest with small numbers of parameters, while `diffeq_adjoint` will
be the fastest when there are large numbers of parameters (like with a
neural ODE).

### Using Other Differential Equations

Other differential equation problem types from DifferentialEquations.jl are
supported. For example, we can build a layer with a delay differential equation
like:

```julia
function delay_lotka_volterra(du,u,h,p,t)
  x, y = u
  α, β, δ, γ = p
  du[1] = dx = (α - β*y)*h(p,t-0.1)[1]
  du[2] = dy = (δ*x - γ)*y
end
h(p,t) = ones(eltype(p),2)
prob = DDEProblem(delay_lotka_volterra,[1.0,1.0],h,(0.0,10.0),constant_lags=[0.1])

p = param([2.2, 1.0, 2.0, 0.4])
params = Flux.Params([p])
function predict_rd_dde()
  Array(diffeq_rd(p,prob,MethodOfSteps(Tsit5()),saveat=0.1))
end
loss_rd_dde() = sum(abs2,x-1 for x in predict_rd_dde())
loss_rd_dde()
```

Or we can use a stochastic differential equation:

```julia
function lotka_volterra_noise(du,u,p,t)
  du[1] = 0.1u[1]
  du[2] = 0.1u[2]
end
prob = SDEProblem(lotka_volterra,lotka_volterra_noise,[1.0,1.0],(0.0,10.0))

p = param([2.2, 1.0, 2.0, 0.4])
params = Flux.Params([p])
function predict_fd_sde()
  diffeq_fd(p,reduction,101,prob,SOSRI(),saveat=0.1)
end
loss_fd_sde() = sum(abs2,x-1 for x in predict_fd_sde())
loss_fd_sde()

data = Iterators.repeated((), 100)
opt = ADAM(0.1)
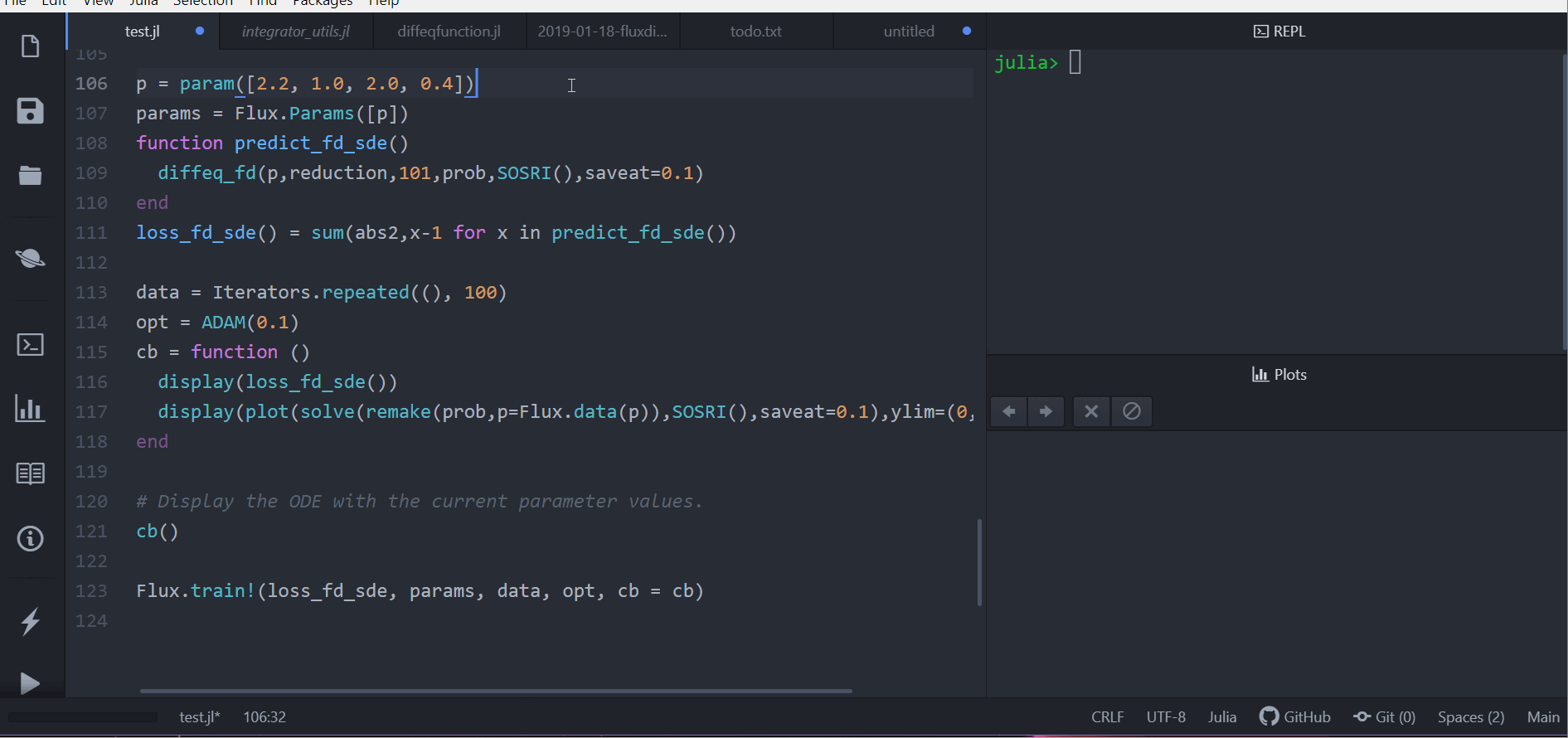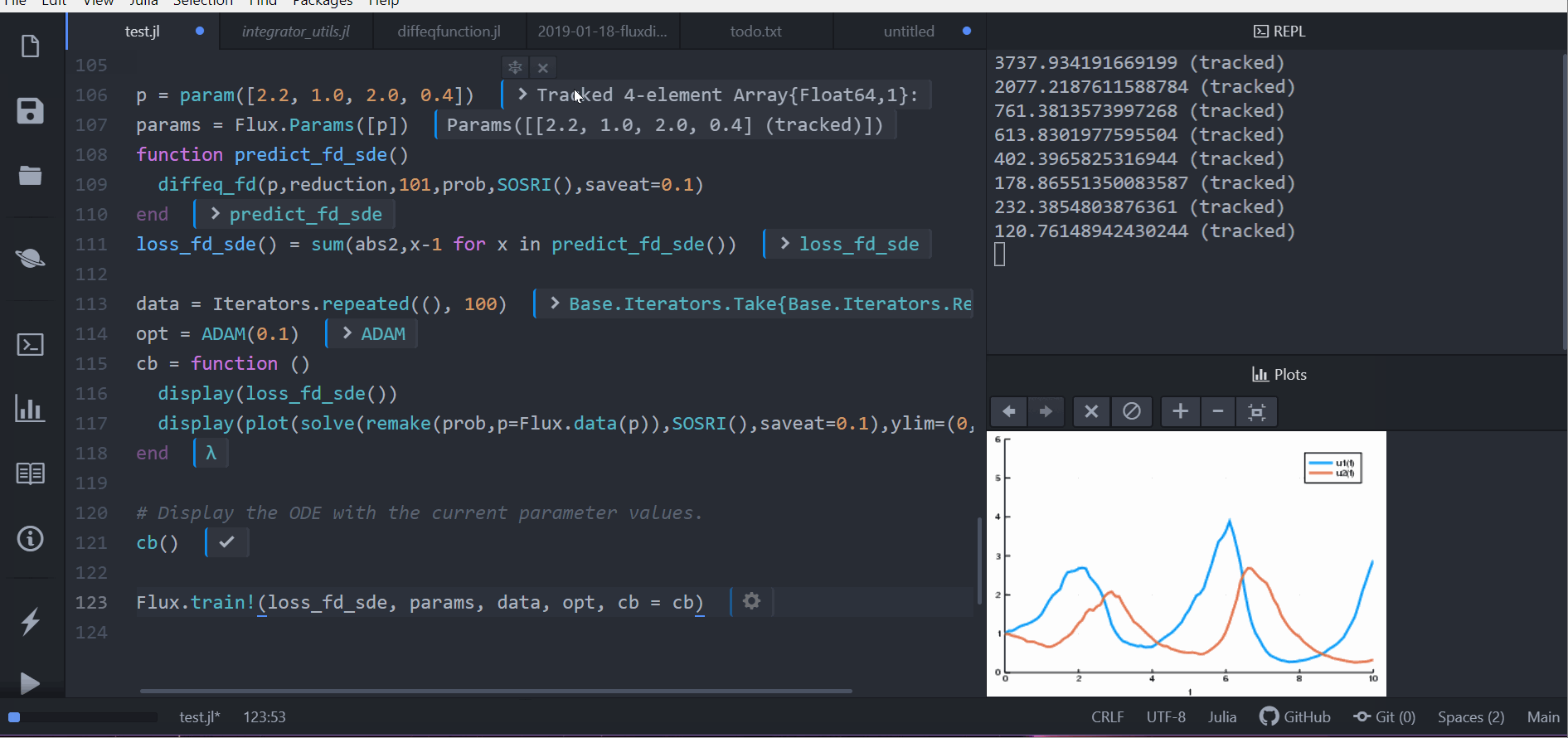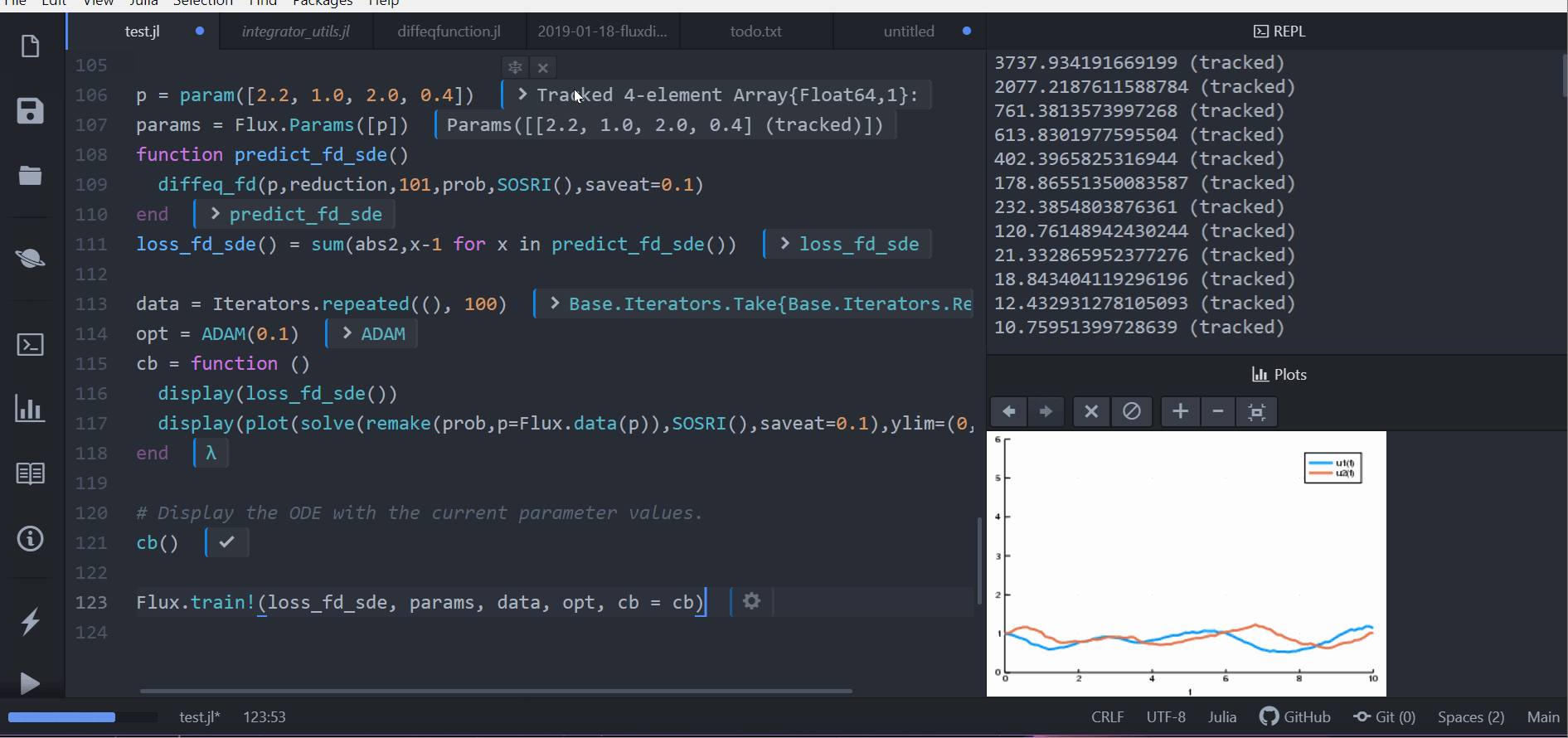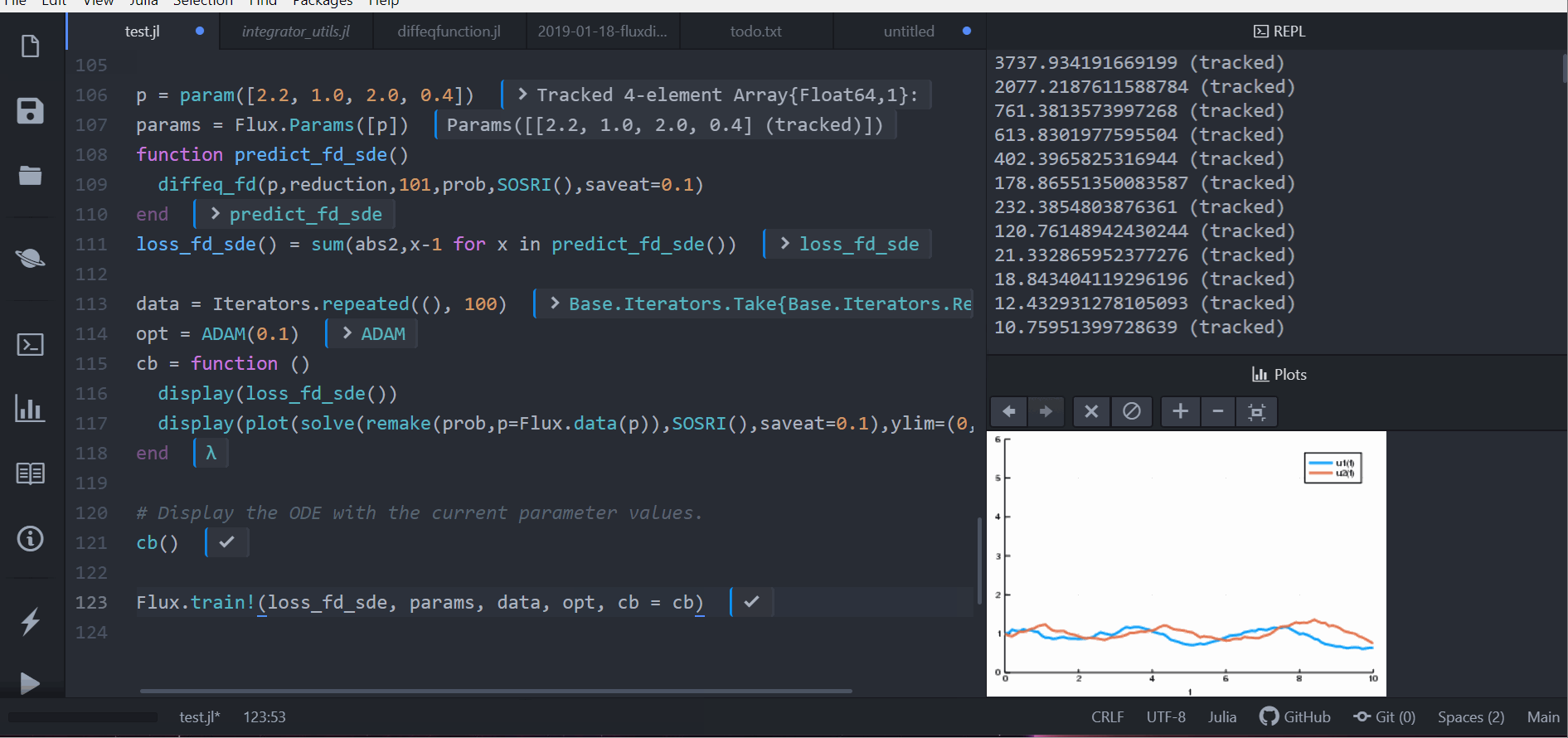
cb = function ()
  display(loss_fd_sde())
  display(plot(solve(remake(prob,p=Flux.data(p)),SOSRI(),saveat=0.1),ylim=(0,6)))
end

# Display the ODE with the current parameter values.
cb()

Flux.train!(loss_fd_sde, params, data, opt, cb = cb)
```

![SDE NN Animation](https://user-images.githubusercontent.com/1814174/51399524-2c6abf80-1b14-11e9-96ae-0192f7debd03.gif)

### Neural Ordinary Differential Equations

We can use DiffEqFlux.jl to define, solve, and train neural ordinary differential
equations. A neural ODE is an ODE where a neural network defines its derivative
function. Thus for example, with the multilayer perceptron neural network
`Chain(Dense(2,50,tanh),Dense(50,2))`, a neural ODE would be defined as having
the ODE function:

```julia
model = Chain(Dense(2,50,tanh),Dense(50,2))
# Define the ODE as the forward pass of the neural network with weights `p`
function dudt(du,u,p,t)
    du .= model(u)
end
```

A convenience function which handles all of the details is `neural_ode`. To
use `neural_ode`, you give it the initial condition, the internal neural
network model to use, the timespan to solve on, and any ODE solver arguments.
For example, this neural ODE would be defined as:

```julia
tspan = (0.0f0,25.0f0)
x -> neural_ode(model,x,tspan,Tsit5(),saveat=0.1)
```

where here we made it a layer that takes in the initial condition and spits
out an array for the time series saved at every 0.1 time steps.

### Training a Neural Ordinary Differential Equation

Let's get a time series array from the Lotka-Volterra equation as data:

```julia
u0 = Float32[2.; 0.]
datasize = 30
tspan = (0.0f0,1.5f0)

function trueODEfunc(du,u,p,t)
    true_A = [-0.1 2.0; -2.0 -0.1]
    du .= ((u.^3)'true_A)'
end
t = range(tspan[1],tspan[2],length=datasize)
prob = ODEProblem(trueODEfunc,u0,tspan)
ode_data = Array(solve(prob,Tsit5(),saveat=t))
```

Now let's define a neural network with a `neural_ode` layer. First we define
the layer:

```julia
dudt = Chain(x -> x.^3,
             Dense(2,50,tanh),
             Dense(50,2))
n_ode(x) = neural_ode(dudt,x,tspan,Tsit5(),saveat=t,reltol=1e-7,abstol=1e-9)
```

And build a neural network around it. We will use the L2 loss of the network's
output against the time series data:

```julia
function predict_n_ode()
  n_ode(u0)
end
loss_n_ode() = sum(abs2,ode_data .- predict_n_ode())
```

and then train the neural network to learn the ODE:

```julia
data = Iterators.repeated((), 1000)
opt = ADAM(0.1)
cb = function () #callback function to observe training
  display(loss_n_ode())
  # plot current prediction against data
  cur_pred = Flux.data(predict_n_ode())
  pl = scatter(t,ode_data[1,:],label="data")
  scatter!(pl,t,cur_pred[1,:],label="prediction")
  display(plot(pl))
end

# Display the ODE with the initial parameter values.
cb()

ps = Flux.params(dudt)
Flux.train!(loss_n_ode, ps, data, opt, cb = cb)
```
## Use with GPUs

Note that the differential equation solvers will run on the GPU if the initial
condition is a GPU array. Thus for example, we can define a neural ODE by hand
that runs on the GPU:

```julia
u0 = [2.; 0.] |> gpu
dudt = Chain(Dense(2,50,tanh),Dense(50,2)) |> gpu

function ODEfunc(du,u,p,t)
    du .= Flux.data(dudt(u))
end
prob = ODEProblem(ODEfunc, u0,tspan)

# Runs on a GPU
sol = solve(prob,Tsit5(),saveat=0.1)
```

and the `diffeq` layer functions can be used similarly. Or we can directly use
the neural ODE layer function, like:

```julia
x -> neural_ode(gpu(dudt),gpu(x),tspan,Tsit5(),saveat=0.1)
```

## Mixed Neural DEs

You can also mix a known differential equation and a neural differential equation, so that
the parameters and the neural network are estimated simultaniously. Here's an example of
doing this with both reverse-mode autodifferentiation and with adjoints:

```julia
using DiffEqFlux, Flux, OrdinaryDiffEq

x = Float32[0.8; 0.8]
tspan = (0.0f0,25.0f0)

ann = Chain(Dense(2,10,tanh), Dense(10,1))
p = param(Float32[-2.0,1.1])

function dudt_(u::TrackedArray,p,t)
    x, y = u
    Flux.Tracker.collect([ann(u)[1],p[1]*y + p[2]*x])
end
function dudt_(u::AbstractArray,p,t)
    x, y = u
    [Flux.data(ann(u)[1]),p[1]*y + p[2]*x*y]
end

prob = ODEProblem(dudt_,x,tspan,p)
diffeq_rd(p,prob,Tsit5())
_x = param(x)

function predict_rd()
  Flux.Tracker.collect(diffeq_rd(p,prob,Tsit5(),u0=_x))
end
loss_rd() = sum(abs2,x-1 for x in predict_rd())
loss_rd()

data = Iterators.repeated((), 10)
opt = ADAM(0.1)
cb = function ()
  display(loss_rd())
  #display(plot(solve(remake(prob,u0=Flux.data(_x),p=Flux.data(p)),Tsit5(),saveat=0.1),ylim=(0,6)))
end

# Display the ODE with the current parameter values.
cb()

Flux.train!(loss_rd, params(ann,p,_x), data, opt, cb = cb)

## Partial Neural Adjoint

u0 = param(Float32[0.8; 0.8])
tspan = (0.0f0,25.0f0)

ann = Chain(Dense(2,10,tanh), Dense(10,1))

p1 = Flux.data(DiffEqFlux.destructure(ann))
p2 = Float32[-2.0,1.1]
p3 = param([p1;p2])
ps = Flux.params(p3,u0)

function dudt_(du,u,p,t)
    x, y = u
    du[1] = DiffEqFlux.restructure(ann,p[1:41])(u)[1]
    du[2] = p[end-1]*y + p[end]*x
end
prob = ODEProblem(dudt_,u0,tspan,p3)
diffeq_adjoint(p3,prob,Tsit5(),u0=u0,abstol=1e-8,reltol=1e-6)

function predict_adjoint()
  diffeq_adjoint(p3,prob,Tsit5(),u0=u0,saveat=0.0:0.1:25.0)
end
loss_adjoint() = sum(abs2,x-1 for x in predict_adjoint())
loss_adjoint()

data = Iterators.repeated((), 10)
opt = ADAM(0.1)
cb = function ()
  display(loss_adjoint())
  #display(plot(solve(remake(prob,p=Flux.data(p3),u0=Flux.data(u0)),Tsit5(),saveat=0.1),ylim=(0,6)))
end

# Display the ODE with the current parameter values.
cb()

Flux.train!(loss_adjoint, ps, data, opt, cb = cb)
```

## API Documentation

### DiffEq Layer Functions

- `diffeq_rd(p,prob, args...;u0 = prob.u0, kwargs...)` uses Flux.jl's
  reverse-mode AD through the differential equation solver with parameters `p`
  and initial condition `u0`. The rest of the arguments are passed to the
  differential equation solver. The return is the DESolution. Note: if you
  use this function, it is much better to use the allocating out of place
  form (`f(u,p,t)` for ODEs) than the in place form (`f(du,u,p,t)` for ODEs)!
- `diffeq_fd(p,reduction,n,prob,args...;u0 = prob.u0, kwargs...)` uses
  ForwardDiff.jl's forward-mode AD through the differential equation solver
  with parameters `p` and initial condition `u0`. `n` is the output size
  where the return value is `reduction(sol)`. The rest of the arguments are
  passed to the differential equation solver.
- `diffeq_adjoint(p,prob,args...;u0 = prob.u0, kwargs...)` uses adjoint
  sensitivity analysis to  "backprop the ODE solver" via DiffEqSensitivity.jl.
  The return is the time series of the solution as an array solved with parameters
  `p` and initial condition `u0`. The rest of the arguments are passed to the
  differential equation solver or handled by the adjoint sensitivity algorithm
  (for more details on sensitivity arguments, see
  [the diffeq documentation](http://docs.juliadiffeq.org/latest/analysis/sensitivity.html#Adjoint-Sensitivity-Analysis-1)).

### Neural DE Layer Functions

- `neural_ode(model,x,tspan,args...;kwargs...)` defines a neural ODE layer where
  `model` is a Flux.jl model, `x` is the initial condition, `tspan` is the
  time span to integrate, and the rest of the arguments are passed to the ODE
  solver. The parameters should be implicit in the `model`.
- `neural_dmsde(model,x,mp,tspan,args...;kwargs)` defines a neural multiplicative
  SDE layer where `model` is a Flux.jl model, `x` is the initial condition, 
  `tspan` is the time span to integrate, and the rest of the arguments are
  passed to the SDE solver. The noise is assumed to be diagonal multiplicative,
  i.e. the Wiener term is `mp.*u.*dW` for some array of noise constants `mp`.