https://github.com/JuliaDiffEq/DiffEqFlux.jl
Tip revision: 20857325436c2a569fc67d50b563df89f0e13648 authored by Christopher Rackauckas on 24 January 2020, 07:55:08 UTC
Update Project.toml
Update Project.toml
Tip revision: 2085732
README.md
# DiffEqFlux.jl
[](https://gitter.im/JuliaDiffEq/Lobby?utm_source=badge&utm_medium=badge&utm_campaign=pr-badge&utm_content=badge)
[](https://travis-ci.org/JuliaDiffEq/DiffEqFlux.jl)
[](https://ci.appveyor.com/project/ChrisRackauckas/diffeqflux-jl)
[](https://gitlab.com/juliadiffeq/DiffEqFlux-jl/pipelines)
DiffEqFlux.jl fuses the world of differential equations with machine learning
by helping users put diffeq solvers into neural networks. This package utilizes
[DifferentialEquations.jl](http://docs.juliadiffeq.org/dev/) and
[Flux.jl](https://fluxml.ai/) as its building blocks to support research in
[Scientific Machine Learning](http://www.stochasticlifestyle.com/the-essential-tools-of-scientific-machine-learning-scientific-ml/)
and neural differential equations in traditional machine learning.
## Problem Domain
DiffEqFlux.jl is not just for neural ordinary differential equations.
DiffEqFlux.jl is for universal differential equations. For an overview of the topic
with applications, consult the paper [Universal Differential Equations for Scientific Machine Learning](https://arxiv.org/abs/2001.04385)
As such, it is the first package to support and demonstrate:
- Stiff universal ordinary differential equations (universal ODEs)
- Universal stochastic differential equations (universal SDEs)
- Universal delay differential equations (universal DDEs)
- Universal partial differential equations (universal PDEs)
- Universal jump stochastic differential equations (universal jump diffusions)
- Hybrid universal differential equations (universal DEs with event handling)
with high order, adaptive, implicit, GPU-accelerated, Newton-Krylov, etc.
methods. For examples, please refer to
[the release blog post](https://julialang.org/blog/2019/01/fluxdiffeq).
Additional demonstrations, like neural
PDEs and neural jump SDEs, can be found
[at this blog post](http://www.stochasticlifestyle.com/neural-jump-sdes-jump-diffusions-and-neural-pdes/)
(among many others!).
Do not limit yourself to the current neuralization. With this package, you can
explore various ways to integrate the two methodologies:
- Neural networks can be defined where the “activations” are nonlinear functions
described by differential equations.
- Neural networks can be defined where some layers are ODE solves
- ODEs can be defined where some terms are neural networks
- Cost functions on ODEs can define neural networks
## Citation
If you use DiffEqFlux.jl or are influenced by its ideas for expanding beyond
neural ODEs, please cite:
```
@article{DBLP:journals/corr/abs-1902-02376,
author = {Christopher Rackauckas and
Mike Innes and
Yingbo Ma and
Jesse Bettencourt and
Lyndon White and
Vaibhav Dixit},
title = {DiffEqFlux.jl - {A} Julia Library for Neural Differential Equations},
journal = {CoRR},
volume = {abs/1902.02376},
year = {2019},
url = {http://arxiv.org/abs/1902.02376},
archivePrefix = {arXiv},
eprint = {1902.02376},
timestamp = {Tue, 21 May 2019 18:03:36 +0200},
biburl = {https://dblp.org/rec/bib/journals/corr/abs-1902-02376},
bibsource = {dblp computer science bibliography, https://dblp.org}
}
```
## Example Usage
For an overview of what this package is for,
[see this blog post](https://julialang.org/blog/2019/01/fluxdiffeq).
### Optimizing parameters of an ODE
First let's create a Lotka-Volterra ODE using DifferentialEquations.jl. For
more details, [see the DifferentialEquations.jl documentation](http://docs.juliadiffeq.org/dev/)
```julia
using DifferentialEquations
function lotka_volterra(du,u,p,t)
x, y = u
α, β, δ, γ = p
du[1] = dx = α*x - β*x*y
du[2] = dy = -δ*y + γ*x*y
end
u0 = [1.0,1.0]
tspan = (0.0,10.0)
p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(lotka_volterra,u0,tspan,p)
sol = solve(prob,Tsit5())
using Plots
plot(sol)
```
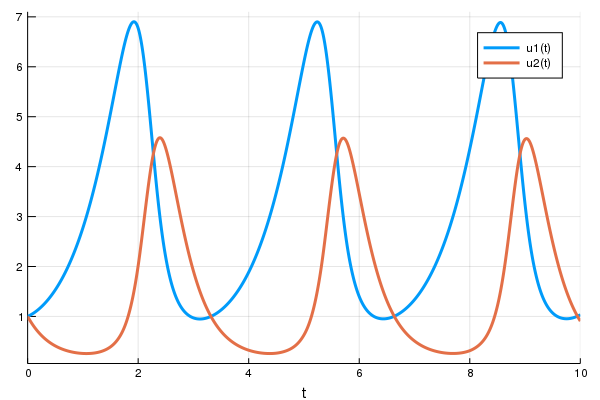
Next we define a single layer neural network that using the
[AD-compatible `concrete_solve` function](https://docs.juliadiffeq.org/latest/analysis/sensitivity/)
function that takes the parameters and an initial condition and returns the
solution of the differential equation as a
[`DiffEqArray`](https://github.com/JuliaDiffEq/RecursiveArrayTools.jl) (same
array semantics as the standard differential equation solution object but without
the interpolations).
```julia
using Flux, DiffEqFlux
p = [2.2, 1.0, 2.0, 0.4] # Initial Parameter Vector
function predict_adjoint() # Our 1-layer neural network
Array(concrete_solve(prob,Tsit5(),u0,p,saveat=0.0:0.1:10.0))
end
```
Next we choose a loss function. Our goal will be to find parameter that make
the Lotka-Volterra solution constant `x(t)=1`, so we defined our loss as the
squared distance from 1:
```julia
loss_adjoint() = sum(abs2,x-1 for x in predict_adjoint())
```
Lastly, we train the neural network using Flux to arrive at parameters which
optimize for our goal:
```julia
data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function () #callback function to observe training
display(loss_adjoint())
# using `remake` to re-create our `prob` with current parameters `p`
display(plot(solve(remake(prob,p=p),Tsit5(),saveat=0.0:0.1:10.0),ylim=(0,6)))
end
# Display the ODE with the initial parameter values.
cb()
Flux.train!(loss_adjoint, Flux.params(p), data, opt, cb = cb)
```
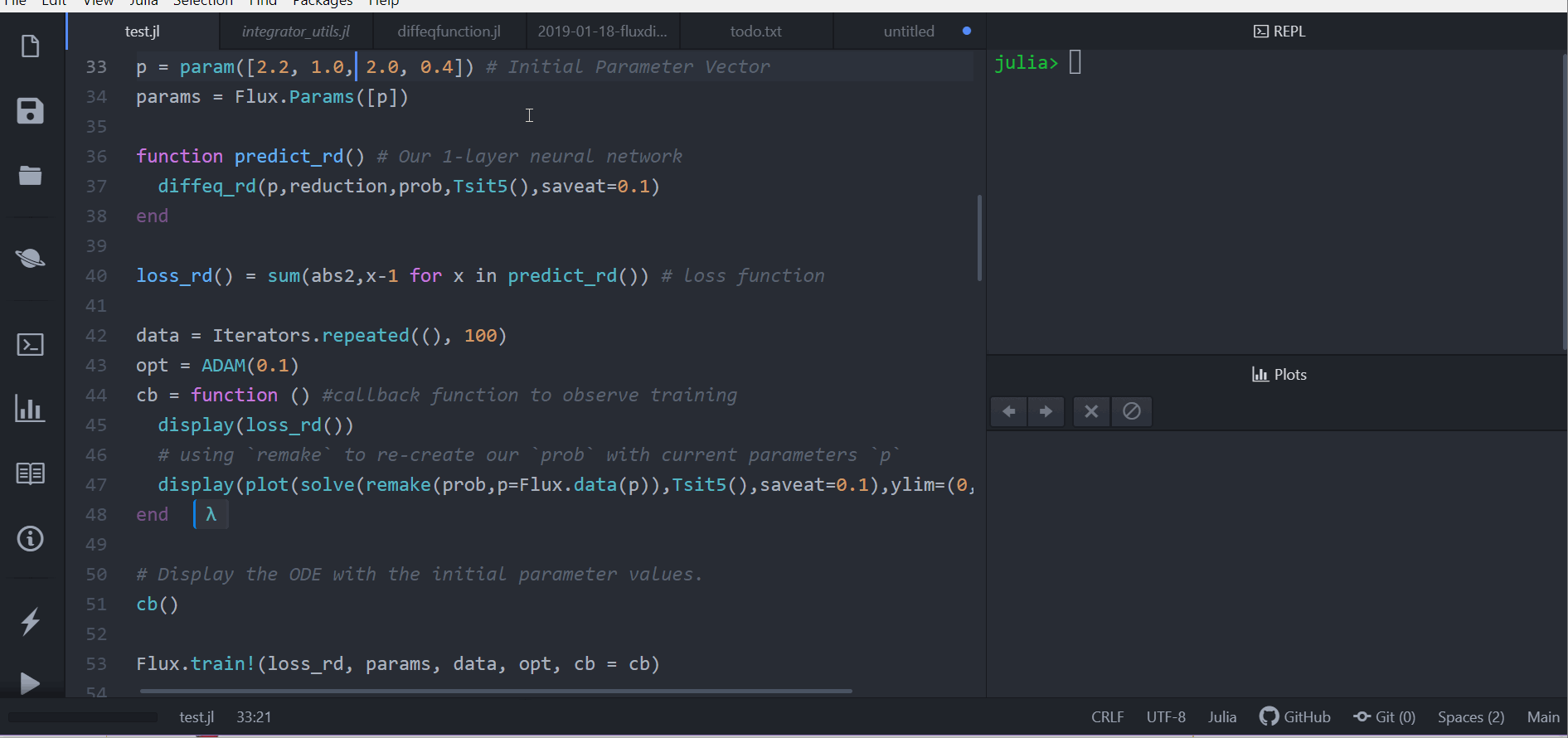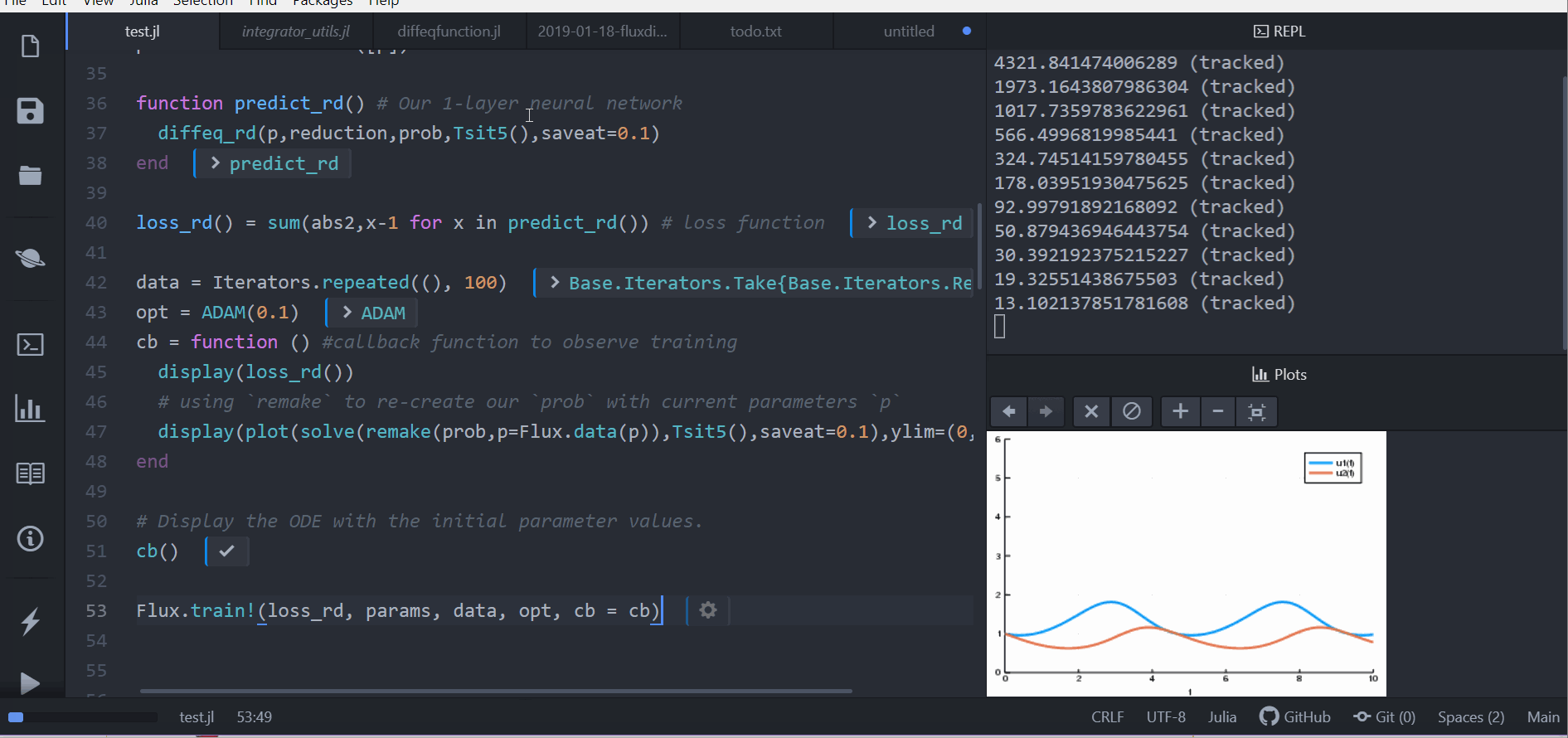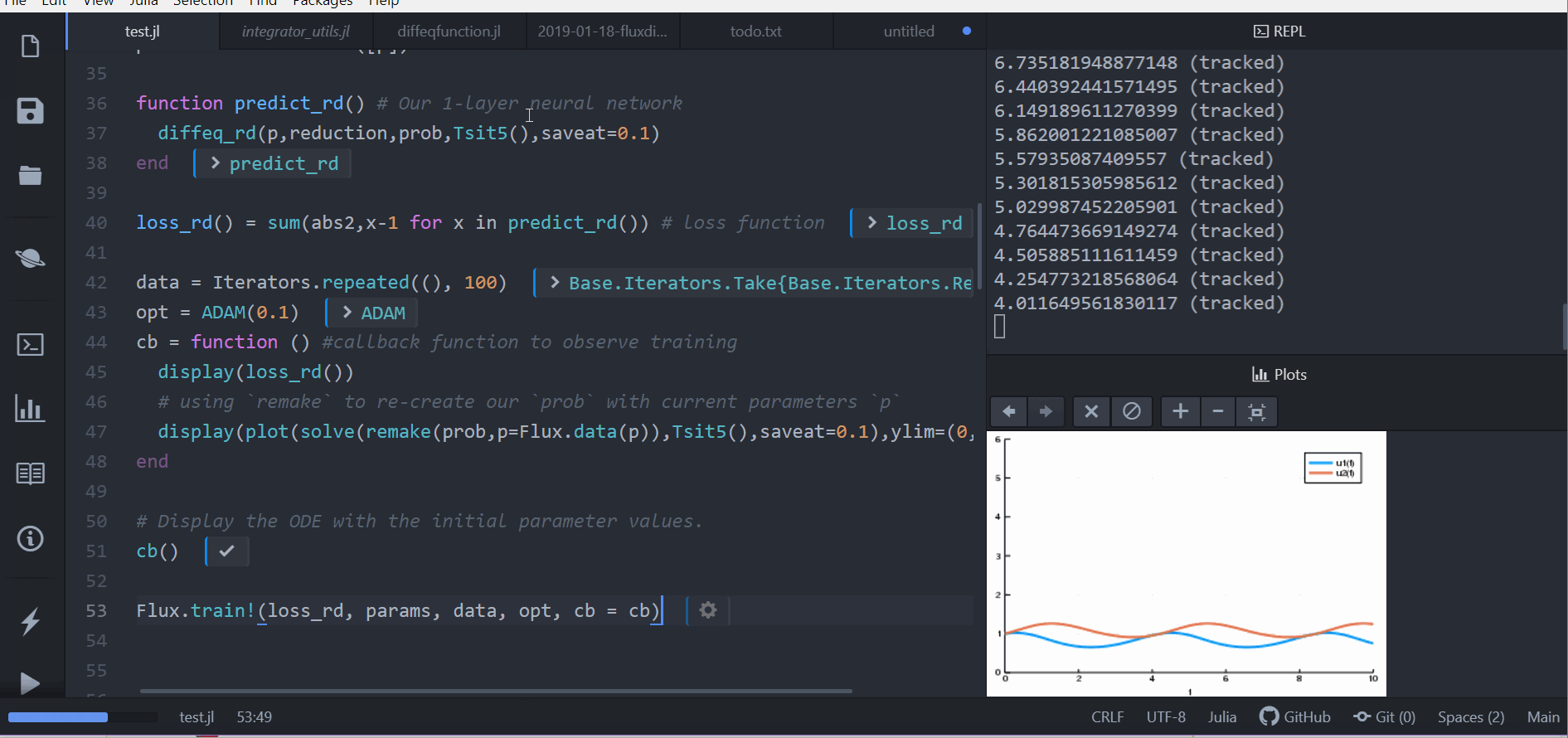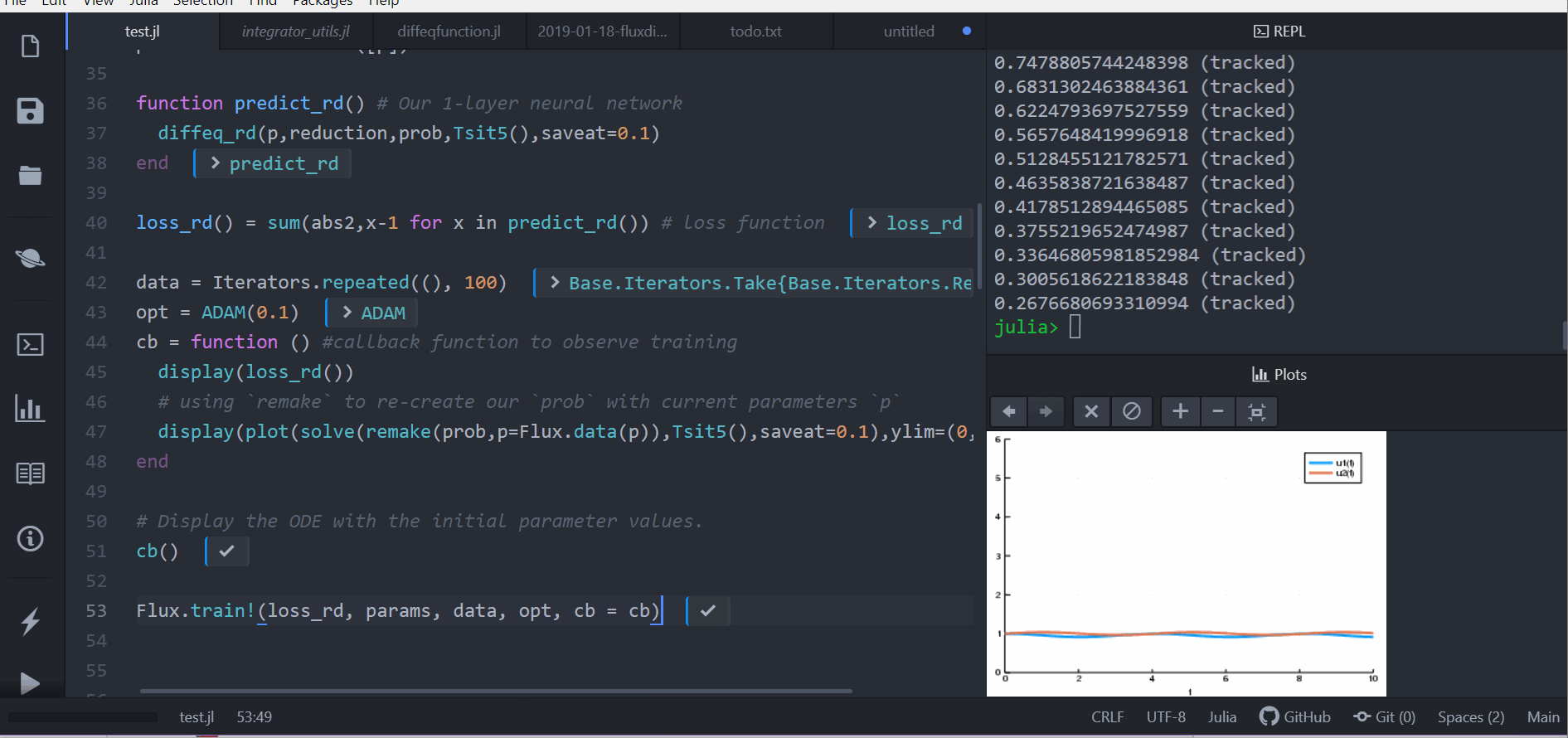
Note that by using anonymous functions, this `diffeq_adjoint` can be used as a
layer in a neural network `Chain`, for example like
```julia
m = Chain(
Conv((2,2), 1=>16, relu),
x -> maxpool(x, (2,2)),
Conv((2,2), 16=>8, relu),
x -> maxpool(x, (2,2)),
x -> reshape(x, :, size(x, 4)),
# takes in the ODE parameters from the previous layer
p -> diffeq_adjoint(p,prob,Tsit5(),saveat=0.1),
Dense(288, 10), softmax) |> gpu
```
or
```julia
m = Chain(
Dense(28^2, 32, relu),
# takes in the initial condition from the previous layer
x -> diffeq_rd(p,prob,Tsit5(),saveat=0.1,u0=x)),
Dense(32, 10),
softmax)
```
Similarly, `diffeq_adjoint`, a O(1) memory adjoint implementation, can be
replaced with `diffeq_rd` for reverse-mode automatic differentiation or
`diffeq_fd` for forward-mode automatic differentiation. `diffeq_fd` will
be fastest with small numbers of parameters, while `diffeq_adjoint` will
be the fastest when there are large numbers of parameters (like with a
neural ODE). See the layer API documentation for details.
### Using Other Differential Equations
Other differential equation problem types from DifferentialEquations.jl are
supported. For example, we can build a layer with a delay differential equation
like:
```julia
function delay_lotka_volterra(du,u,h,p,t)
x, y = u
α, β, δ, γ = p
du[1] = dx = (α - β*y)*h(p,t-0.1)[1]
du[2] = dy = (δ*x - γ)*y
end
h(p,t) = ones(eltype(p),2)
u0 = [1.0,1.0]
prob = DDEProblem(delay_lotka_volterra,u0,h,(0.0,10.0),constant_lags=[0.1])
p = [2.2, 1.0, 2.0, 0.4]
function predict_dde()
Array(concrete_solve(prob,MethodOfSteps(Tsit5()),u0,p,saveat=0.1,sensealg=TrackerAdjoint())
end
loss_dde() = sum(abs2,x-1 for x in predict_dde())
loss_dde()
```
Notice that we chose `sensealg=ForwardDiffSensitivity()` to utilize the ForwardDiff.jl
forward-mode to handle a small delay differential equation, a strategy that can
be good for small equations (see the performance discussion for more details
on other forms).
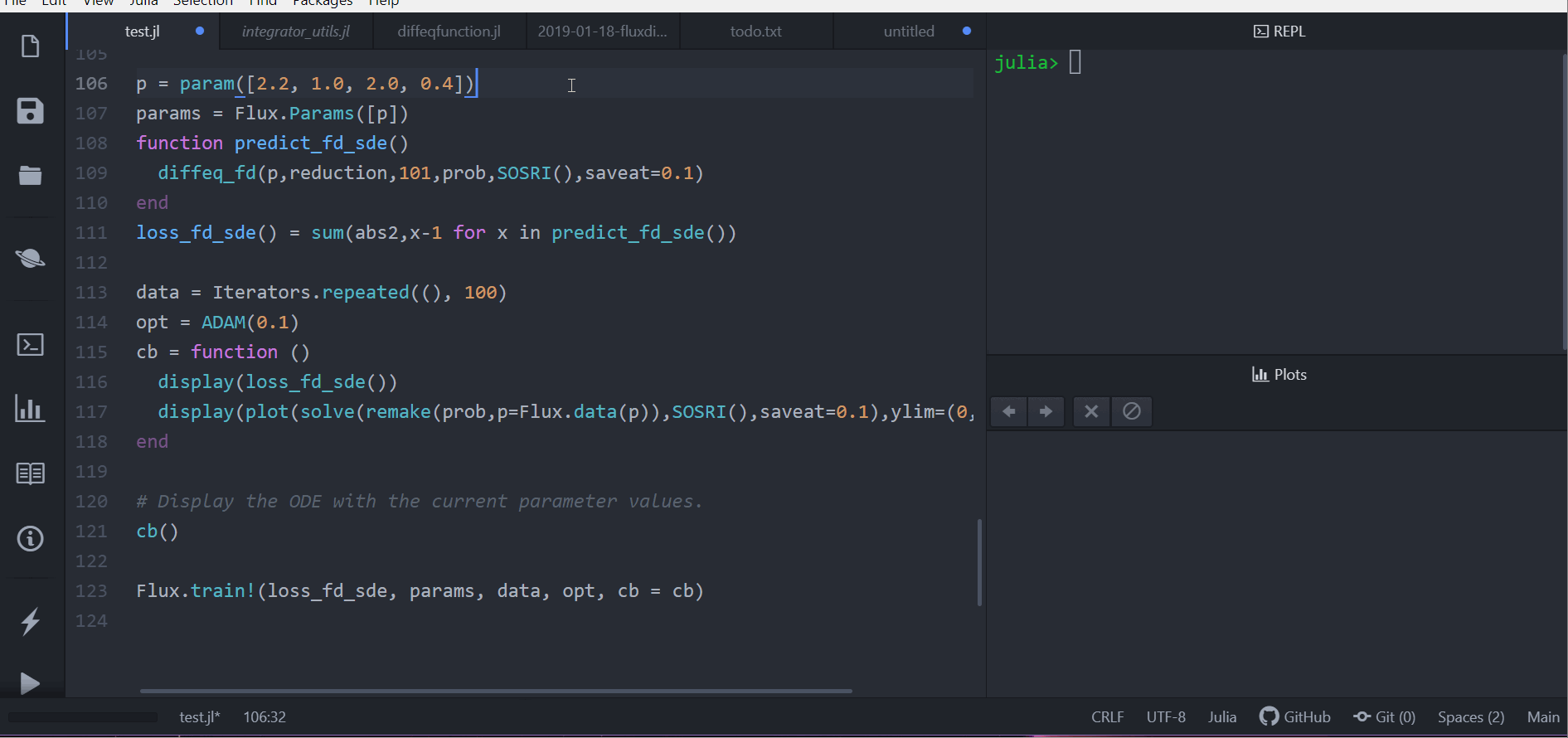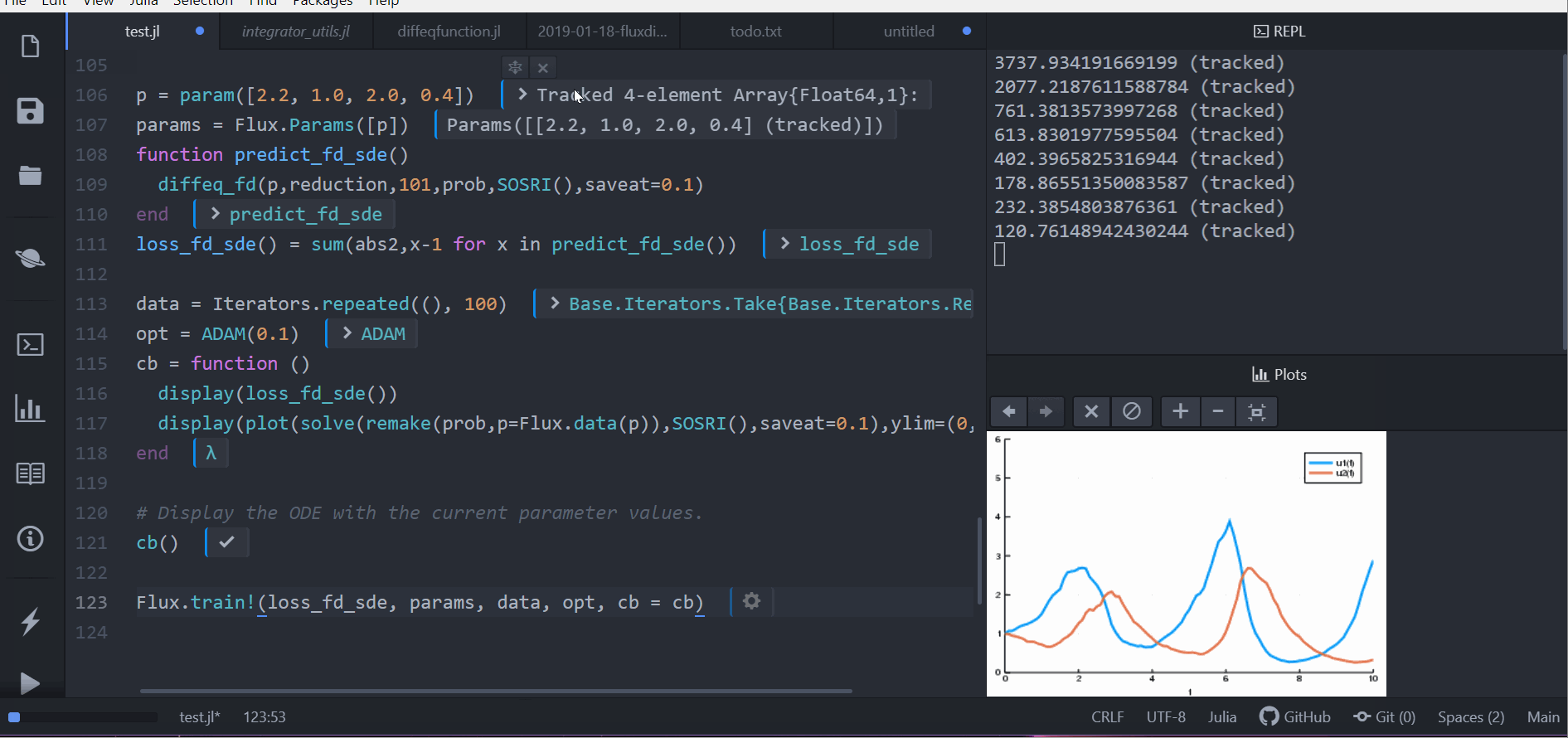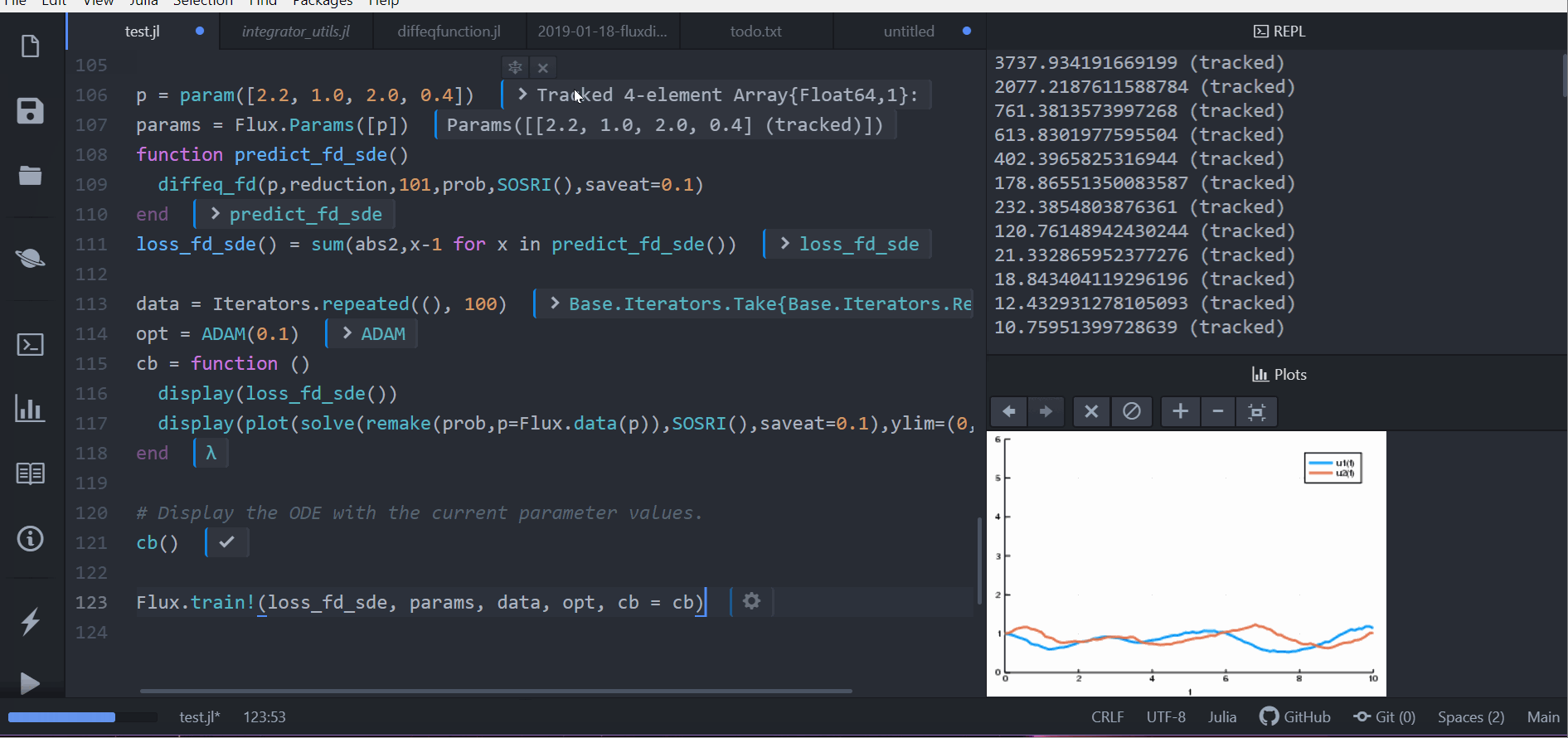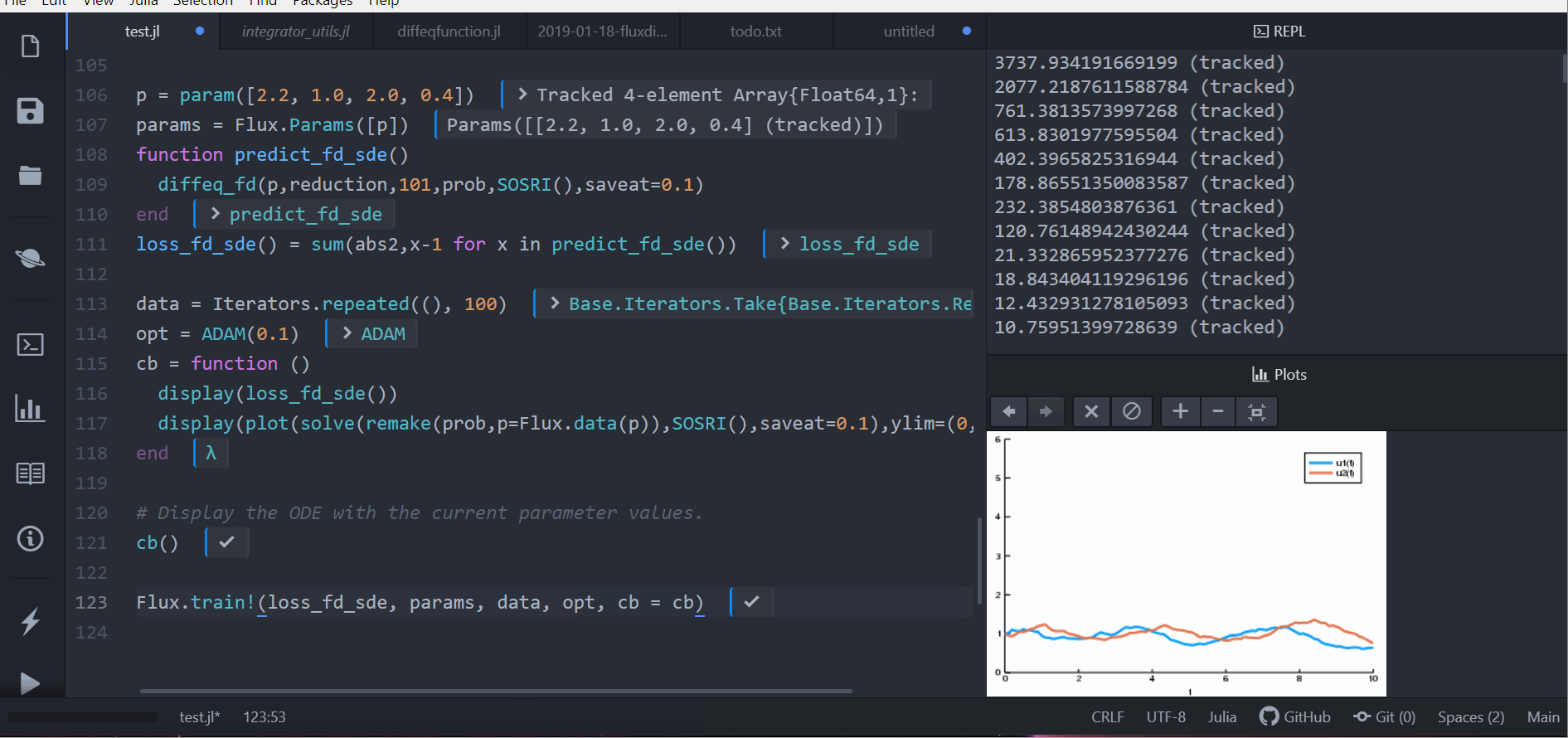
Or we can use a stochastic differential equation. Here we demonstrate
`sensealg=TrackerAdjoint()` for reverse-mode automatic differentiation
of a small differential equation:
```julia
function lotka_volterra_noise(du,u,p,t)
du[1] = 0.1u[1]
du[2] = 0.1u[2]
end
u0 = [1.0,1.0]
prob = SDEProblem(lotka_volterra,lotka_volterra_noise,u0,(0.0,10.0))
p = [2.2, 1.0, 2.0, 0.4]
function predict_sde()
Array(concrete_solve(prob,SOSRI,u0,p,sensealg=TrackerAdjoint(),saveat=0.1))
end
loss_sde() = sum(abs2,x-1 for x in predict_sde())
loss_sde()
data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function ()
display(loss_sde())
display(plot(solve(remake(prob,p=p),SOSRI(),saveat=0.1),ylim=(0,6)))
end
# Display the ODE with the current parameter values.
cb()
Flux.train!(loss_sde, Flux.params(p), data, opt, cb = cb)
```
### Neural Ordinary Differential Equations
We can use DiffEqFlux.jl to define, solve, and train neural ordinary differential
equations. A neural ODE is an ODE where a neural network defines its derivative
function. Thus for example, with the multilayer perceptron neural network
`Chain(Dense(2,50,tanh),Dense(50,2))`, the best way to define a neural ODE by hand
would be to use non-mutating adjoints, which looks like:
```julia
p,re = Flux.destructure(model)
dudt_(u,p,t) = re(p)(u)
prob = ODEProblem(dudt_,x,tspan,p)
my_neural_ode_prob = concrete_solve(prob,Tsit5(),u0,p,args...;kwargs...)
```
(`Flux.restructure` and `Flux.destructure` are helper functions which transform
the neural network to use parameters `p`)
A convenience function which handles all of the details is `NeuralODE`. To
use `NeuralODE`, you give it the initial condition, the internal neural
network model to use, the timespan to solve on, and any ODE solver arguments.
For example, this neural ODE would be defined as:
```julia
tspan = (0.0f0,25.0f0)
n_ode = NeuralODE(model,tspan,Tsit5(),saveat=0.1)
```
where here we made it a layer that takes in the initial condition and spits
out an array for the time series saved at every 0.1 time steps.
### Training a Neural Ordinary Differential Equation
Let's get a time series array from the Lotka-Volterra equation as data:
```julia
u0 = Float32[2.; 0.]
datasize = 30
tspan = (0.0f0,1.5f0)
function trueODEfunc(du,u,p,t)
true_A = [-0.1 2.0; -2.0 -0.1]
du .= ((u.^3)'true_A)'
end
t = range(tspan[1],tspan[2],length=datasize)
prob = ODEProblem(trueODEfunc,u0,tspan)
ode_data = Array(solve(prob,Tsit5(),saveat=t))
```
Now let's define a neural network with a `neural_ode` layer. First we define
the layer:
```julia
dudt2 = Chain(x -> x.^3,
Dense(2,50,tanh),
Dense(50,2))
n_ode = NeuralODE(dudt2,tspan,Tsit5(),saveat=t)
```
Here we used the `x -> x.^3` assumption in the model. By incorporating structure
into our equations, we can reduce the required size and training time for the
neural network, but a good guess needs to be known!
From here we build a loss function around it. We will use the L2 loss of the network's
output against the time series data:
```julia
function predict_n_ode()
n_ode(u0)
end
loss_n_ode() = sum(abs2,ode_data .- predict_n_ode())
```
and then train the neural network to learn the ODE:
```julia
data = Iterators.repeated((), 1000)
opt = ADAM(0.1)
cb = function () #callback function to observe training
display(loss_n_ode())
# plot current prediction against data
cur_pred = predict_n_ode()
pl = scatter(t,ode_data[1,:],label="data")
scatter!(pl,t,cur_pred[1,:],label="prediction")
display(plot(pl))
end
# Display the ODE with the initial parameter values.
cb()
ps = Flux.params(n_ode)
# or train the initial condition and neural network
# ps = Flux.params(u0,dudt)
Flux.train!(loss_n_ode, ps, data, opt, cb = cb)
```
## Use with GPUs
Note that the differential equation solvers will run on the GPU if the initial
condition is a GPU array. Thus for example, we can define a neural ODE by hand
that runs on the GPU:
```julia
u0 = Float32[2.; 0.] |> gpu
dudt = Chain(Dense(2,50,tanh),Dense(50,2)) |> gpu
p,re = DiffEqFlux.destructure(model)
dudt_(u,p,t) = re(p)(u)
prob = ODEProblem(ODEfunc, u0,tspan, p)
# Runs on a GPU
sol = solve(prob,Tsit5(),saveat=0.1)
```
and the `diffeq` layer functions can be used similarly. Or we can directly use
the neural ODE layer function, like:
```julia
n_ode = NeuralODE(gpu(dudt2),tspan,Tsit5(),saveat=0.1)
```
## Universal Differential Equations
You can also mix a known differential equation and a neural differential equation, so that
the parameters and the neural network are estimated simultaniously. Here's an example of
doing this with both reverse-mode autodifferentiation and with adjoints:
```julia
using DiffEqFlux, Flux, OrdinaryDiffEq
## --- Partial Neural Adjoint ---
u0 = Float32[0.8; 0.8]
tspan = (0.0f0,25.0f0)
ann = Chain(Dense(2,10,tanh), Dense(10,1))
p1,re = Flux.destructure(ann)
p2 = Float32[-2.0,1.1]
p3 = [p1;p2]
ps = Flux.params(p3,u0)
function dudt_(du,u,p,t)
x, y = u
du[1] = re(p[1:41])(u)[1]
du[2] = p[end-1]*y + p[end]*x
end
prob = ODEProblem(dudt_,u0,tspan,p3)
concrete_solve(prob,Tsit5(),u0,p3,abstol=1e-8,reltol=1e-6)
function predict_adjoint()
Array(concrete_solve(prob,Tsit5(),u0,p3,saveat=0.0:0.1:25.0,abstol=1e-8,reltol=1e-6))
end
loss_adjoint() = sum(abs2,x-1 for x in predict_adjoint())
loss_adjoint()
data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function ()
display(loss_adjoint())
#display(plot(solve(remake(prob,p=p3,u0=u0),Tsit5(),saveat=0.1),ylim=(0,6)))
end
# Display the ODE with the current parameter values.
cb()
Flux.train!(loss_adjoint, ps, data, opt, cb = cb)
```
### Training Universal Differential Equations with Optim's BFGS
In many scientific computing cases, like what we see with Universal Differential Equations,
the classic `BFGS` or `L-BFGS` methods more stable than the methods commonly used in neural
networks. Thus for better fitting we can utilize [Optim.jl](https://github.com/JuliaNLSolvers/Optim.jl)
and tell it to train using the BFGS method. An example of this is as follows:
```julia
using DiffEqFlux, Flux, OrdinaryDiffEq, Optim, Zygote
u0 = Float32[0.8; 0.8]
tspan = (0.0f0,25.0f0)
ann = Chain(Dense(2,10,tanh), Dense(10,1))
p1,re = Flux.destructure(ann)
p2 = Float32[0.5,-0.5]
p3 = [p1;p2]
ptrain = [p3;u0]
function dudt_(du,u,p,t)
x, y = u
du[1] = re(p[1:41])(u)[1]
du[2] = p[end-1]*y + p[end]*x
end
prob = ODEProblem(dudt_,u0,tspan,p3)
concrete_solve(prob,Tsit5(),u0,p3,abstol=1e-8,reltol=1e-6)
function predict_adjoint(fullp)
Array(concrete_solve(prob,Tsit5(),fullp[end-1:end],fullp[1:end-1],saveat=0.0:0.1:25.0,abstol=1e-8,reltol=1e-6))
end
loss_adjoint(fullp) = sum(abs2,x-1 for x in predict_adjoint(fullp))
loss_adjoint(ptrain)
function loss_adjoint_gradient!(G, fullp)
G .= Zygote.gradient(loss_adjoint,fullp)[1]
end
optimize(loss_adjoint, loss_adjoint_gradient!, ptrain, BFGS())
```
```
* Status: success
* Candidate solution
Minimizer: [2.94e-01, -3.52e-01, 4.39e-01, ...]
Minimum: 4.463629e-11
* Found with
Algorithm: BFGS
Initial Point: [3.13e-01, -3.43e-01, 3.38e-01, ...]
* Convergence measures
|x - x'| = 0.00e+00 ≤ 0.0e+00
|x - x'|/|x'| = 0.00e+00 ≤ 0.0e+00
|f(x) - f(x')| = 0.00e+00 ≤ 0.0e+00
|f(x) - f(x')|/|f(x')| = 0.00e+00 ≤ 0.0e+00
|g(x)| = 2.46e-05 ≰ 1.0e-08
* Work counters
Seconds run: 202 (vs limit Inf)
Iterations: 30
f(x) calls: 140
∇f(x) calls: 140
```
Notice that in just 30 iterations we get to a minimum of `4e-11`! This is much faster than
methods like ADAM or SGD.
## Neural Differential Equations for Non-ODEs: Neural SDEs, Neural DDEs, etc.
With neural stochastic differential equations, there is once again a helper form `neural_dmsde` which can
be used for the multiplicative noise case (consult the layers API documentation, or
[this full example using the layer function](https://github.com/MikeInnes/zygote-paper/blob/master/neural_sde/neural_sde.jl)).
However, since there are far too many possible combinations for the API to
support, in many cases you will want to performantly define neural differential
equations for non-ODE systems from scratch. For these systems, it is generally
best to use `TrackerAdjoint` with non-mutating (out-of-place) forms. For example,
the following defines a neural SDE with neural networks for both the drift and
diffusion terms:
```julia
dudt_(u,p,t) = model(u)
g(u,p,t) = model2(u)
prob = SDEProblem(dudt_,g,x,tspan,nothing)
```
where `model` and `model2` are different neural networks. The same can apply to a neural delay differential equation.
Its out-of-place formulation is `f(u,h,p,t)`. Thus for example, if we want to define a neural delay differential equation
which uses the history value at `p.tau` in the past, we can define:
```julia
dudt_(u,h,p,t) = model([u;h(t-p.tau)])
prob = DDEProblem(dudt_,u0,h,tspan,nothing)
```
### Neural SDE Example
First let's build training data from the same example as the neural ODE:
```julia
using Flux, DiffEqFlux, StochasticDiffEq, Plots, DiffEqBase.EnsembleAnalysis
u0 = Float32[2.; 0.]
datasize = 30
tspan = (0.0f0,1.0f0)
function trueSDEfunc(du,u,p,t)
true_A = [-0.1 2.0; -2.0 -0.1]
du .= ((u.^3)'true_A)'
end
t = range(tspan[1],tspan[2],length=datasize)
mp = Float32[0.2,0.2]
function true_noise_func(du,u,p,t)
du .= mp.*u
end
prob = SDEProblem(trueSDEfunc,true_noise_func,u0,tspan)
```
For our dataset we will use DifferentialEquations.jl's [parallel ensemble interface](http://docs.juliadiffeq.org/dev/features/ensemble.html)
to generate data from the average of 10000 runs of the SDE:
```julia
# Take a typical sample from the mean
ensemble_prob = EnsembleProblem(prob)
ensemble_sol = solve(ensemble_prob,SOSRI(),trajectories = 10000)
ensemble_sum = EnsembleSummary(ensemble_sol)
sde_data,sde_data_vars = Array.(timeseries_point_meanvar(ensemble_sol,t))
```
Now we build a neural SDE. For simplicity we will use the `NueralDSDE`
neural SDE with diagonal noise layer function:
```julia
drift_dudt = Chain(x -> x.^3,
Dense(2,50,tanh),
Dense(50,2))
diffusion_dudt = Chain(Dense(2,2))
n_sde = NeuralDSDE(drift_dudt,diffusion_dudt,tspan,SOSRI(),saveat=t,reltol=1e-1,abstol=1e-1)
ps = Flux.params(n_sde)
```
Let's see what that looks like:
```julia
pred = n_sde(u0) # Get the prediction using the correct initial condition
p1,re1 = Flux.destructure(drift_dudt)
p2,re2 = Flux.destructure(diffusion_dudt)
drift_(u,p,t) = re1(n_sde.p[1:n_sde.len])(u)
diffusion_(u,p,t) = re2(n_sde.p[(n_sde.len+1):end])(u)
nprob = SDEProblem(drift_,diffusion_,u0,(0.0f0,1.2f0),nothing)
ensemble_nprob = EnsembleProblem(nprob)
ensemble_nsol = solve(ensemble_nprob,SOSRI(),trajectories = 100, saveat = t)
ensemble_nsum = EnsembleSummary(ensemble_nsol)
p1 = plot(ensemble_nsum, title = "Neural SDE: Before Training")
scatter!(p1,t,sde_data',lw=3)
scatter(t,sde_data[1,:],label="data")
scatter!(t,pred[1,:],label="prediction")
```
Now just as with the neural ODE we define a loss function that calculates the
mean and variance from `n` runs at each time point and uses the distance
from the data values:
```julia
function predict_n_sde()
Array(n_sde(u0))
end
function loss_n_sde(;n=100)
samples = [predict_n_sde() for i in 1:n]
means = reshape(mean.([[samples[i][j] for i in 1:length(samples)] for j in 1:length(samples[1])]),size(samples[1])...)
vars = reshape(var.([[samples[i][j] for i in 1:length(samples)] for j in 1:length(samples[1])]),size(samples[1])...)
sum(abs2,sde_data - means) + sum(abs2,sde_data_vars - vars)
end
opt = ADAM(0.025)
cb = function () #callback function to observe training
sample = predict_n_sde()
# loss against current data
display(sum(abs2,sde_data .- sample))
# plot current prediction against data
pl = scatter(t,sde_data[1,:],label="data")
scatter!(pl,t,sample[1,:],label="prediction")
display(plot(pl))
end
# Display the SDE with the initial parameter values.
cb()
```
Now we train using this loss function. We can pre-train a little bit using
a smaller `n` and then decrease it after it has had some time to adjust towards
the right mean behavior:
```julia
Flux.train!(()->loss_n_sde(n=10), ps, Iterators.repeated((), 100), opt, cb = cb)
Flux.train!(loss_n_sde, ps, Iterators.repeated((), 100), opt, cb = cb)
```
And now we plot the solution to an ensemble of the trained neural SDE:
```julia
ensemble_nprob = EnsembleProblem(nprob)
ensemble_nsol = solve(ensemble_nprob,SOSRI(),trajectories = 100, saveat =t )
ensemble_nsum = EnsembleSummary(ensemble_nsol)
p2 = scatter(t,sde_data')
plot!(p2,ensemble_nsum, title = "Neural SDE: After Training", xlabel="Time")
scatter!(p2,t,sde_data',lw=3)
plot(p1,p2,layout=(2,1))
```

Try this with GPUs as well!
### Neural Jump Diffusions (Neural Jump SDE) and Neural Partial Differential Equations (Neural PDEs)
For the sake of not having a never-ending documentation of every single combination of CPU/GPU with
every layer and every neural differential equation, we will end here. But you may want to consult
[this blog post](http://www.stochasticlifestyle.com/neural-jump-sdes-jump-diffusions-and-neural-pdes/) which
showcases defining neural jump diffusions and neural partial differential equations.
## API Documentation
### Neural DE Layer Functions
- `NeuralODE(model,tspan,solver,args...;kwargs...)`defines a neural ODE
layer where `model` is a Flux.jl model, `tspan` is the
time span to integrate, and the rest of the arguments are passed to the ODE
solver.
- `NeuralDSDE(model1,model2,tspan,solver,args...;kwargs...)` defines a neural
SDE layer where `model1` is a Flux.jl for the drift equation, `model2` is a
Flux.jl model for the diffusion equation, `tspan` is the time span to
integrate, and the rest of the arguments are passed to the SDE solver.
The noise is diagonal, i.e. it assumes a vector output and performs
`model2(u) .* dW` against a dW matching the number of states.
- `NeuralSDE(model1,model2,tspan,nbrown,solver,args...;kwargs...)` defines a neural
SDE layer where `model1` is a Flux.jl for the drift equation, `model2` is a
Flux.jl model for the diffusion equation, `tspan` is the time span to
integrate, `nbrown` is the number of Brownian motions, and the rest of the
arguments are passed to the SDE solver. The model is multiplicative,
i.e. it's interpreted as `model2(u) * dW`, and so the return of `model2` should
be an appropriate matrix for performing this multiplication, i.e. the size of
its output should be `length(x) x nbrown`.
- `NeuralCDDE(model,tspan,lags,solver,args...;kwargs...)`defines a neural DDE
layer where `model` is a Flux.jl model, `tspan` is the
time span to integrate, lags is the lagged values to use in the predictor,
and the rest of the arguments are passed to the ODE solver. The model should
take in a vector that concatenates the lagged states, i.e.
`[u(t);u(t-lags[1]);...;u(t-lags[end])]`
## Benchmarks
A raw ODE solver benchmark showcases [a 50,000x performance advantage over torchdiffeq on small ODEs](https://gist.github.com/ChrisRackauckas/cc6ac746e2dfd285c28e0584a2bfd320).

